Sentido numérico: el segundo pilar

07/02/201807/10/2020 Rebeca Ascencio46 comentarios

En la entrada pasada, que pueden leer aquí, mencioné que considero que los dos pilares de una buena relación con las matemáticas son el pensamiento lógico matemático y el sentido numérico. Lo concibo así: el pensamiento lógico matemático permite entender rápido y bien qué debe hacerse y el sentido numérico permite elegir las mejores estrategias para hacer cálculos rápido y bien. Dediqué esa entrada al primer pilar, dedicaré ésta al segundo.

Sentido numérico: elegir las mejores estrategias para calcular

Más que una definición de sentido numérico, lo que podemos encontrar en la literatura son características del mismo. Los componentes que la National Council of Teachers of Mathematics (NTCM) identificó en 1989 son los siguientes: entender el significado de los números, las múltiples relaciones entre ellos, sus magnitudes relativas, los efectos de las operaciones y los referentes para medir objetos comunes.

Dicho de una forma más simple, quien ha desarrollado bien su sentido numérico se ha familiarizado tanto con los números y las relaciones entre ellos que sabe cómo realizar el mismo cálculo mediante distintos procedimientos y puede escoger el mejor de ellos para llegar al resultado correcto de forma rápida.

¿Por qué es importante el sentido numérico?

Veamos un ejemplo de elección de estrategias para comprender mejor la importancia del sentido numérico:
En 1994 Eddie Gray y David Tall identificaron una importante causa de las dificultades de los estudiantes con las matemáticas al observar a estudiantes de siete a trece años hacer algunas sumas, sin usar lápiz ni papel y notar que se usaban diferentes procedimientos para hacerlo. Lógicamente, los mejores procedimientos eran usados por los estudiantes que solían tener los mejores desempeños y viceversa. Por ejemplo, al sumar 6 + 17 objetos, estas serían las formas de sumar que ellos clasificaron:

Contar todo: los estudiantes cuentan 6 objetos, luego cuentan 17, luego cuentan todos, desde el principio hasta el final, hasta llegar al 23 (si todo va bien al contar, claro).

Contar a partir del primero: después de contar 6 y 17 por separado, los alumnos ya saben que hay 6 objetos en el primer grupo y cuentan los otros 17 a partir del siguiente número: 7, 8, 9…, hasta llegar al 23 (también depende de que cuenten bien).

Contar a partir del mayor: similar al anterior, pero contando a partir del 18, 19, 20… 23

Hechos conocidos: los estudiantes han hecho antes esa operación y recuerdan el resultado (depende de que ya la hayan hecho y recuerden el resultado).

Hechos derivados de hechos conocidos: en este caso hay más de una forma en que los alumnos pueden hacer la suma, veamos dos ejemplos:

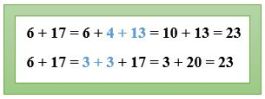Descomponen el 17 en 13 + 4, suman el 6 con el 4 y luego suman el 10 que obtuvieron con el 13 que les había quedado, para llegar a 23.

Descomponen el 6 en 3 + 3, suman un 3 al 17 para llegar a 20 y luego suman el otro 3, para llegar a 23.

El proceder de esta última forma muestra que el alumno ha desarrollado el sentido numérico. Fue observado principalmente en aquellos que mostraban un buen desempeño, lo que puede interpretarse como que tal desempeño depende tanto del procedimiento elegido para hacer la operación como de la habilidad para realizar ese procedimiento.

Si bien las otras formas de sumar son necesarias en las primeras etapas del aprendizaje de la suma, deben ser sustituidas por esta última lo más pronto posible. De esa forma se podrán seguir desarrollando nuevas habilidades matemáticas a buen ritmo.

Puede notarse que para operar usando el sentido numérico se requiere descomponer y recomponer números como mejor convenga para realizar la operación pedida a través de operaciones más sencillas. Se involucra una comprensión profunda de las partes en las que se puede partir cada número y las implicaciones para la operación que se desea realizar. Para el ejemplo, separar el 6 en 2 + 4 no resulta tan útil como separarlo en 3 + 3.

También se requiere creatividad y flexibilidad de pensamiento para buscar entre las posibles opciones, a la vez que se evitan los algoritmos sin sentido, esto es, procedimientos seguidos al pie de la letra sin entender por qué funcionan. Sí, también lo sé, al igual que con el pensamiento lógico matemático, el desarrollo del sentido numérico sirve para mucho más que tener buenos resultados en matemáticas.

¿Por qué, si hace más de 20 años se observó esto, casi no se fomenta intencionadamente en casa y en clase el sentido numérico? No estoy segura, pero creo que en algún punto la difusión de los resultados de las investigaciones se estanca y por ello no llegan a divulgarse entre profesores y papás tan ampliamente como debieran. Tratar de contrarrestar ese estancamiento de la información es uno de los objetivos de este blog.

Una idea para desarrollarlo

Una vez comprendido por qué conviene desarrollar el sentido numérico, pasemos a algo práctico. Les presento en esta entrada una actividad muy sencilla, que toma poco tiempo y puede hacerse tanto con uno o varios hijos como con un grupo completo de alumnos. Se trata de una actividad que prepara al alumno para realizar posteriores descomposiciones y recomposiciones de números, como las mostradas en el apartado anterior.

Para comenzar, se elige un número y se pide a los alumnos que vayan dando, uno por uno, en voz alta, opciones de operaciones, todas diferentes, a partir de otros números, para llegar al número dado. Esta actividad tiene la enorme ventaja de que todos los alumnos pueden encontrar fácilmente una opción diferente a la de los demás. Los que les falta desarrollar la habilidad darán opciones sencillas y los más creativos o hábiles encontrarán opciones más elaboradas. Nadie se quedará sin aportar, eso motiva mucho y todos expandirán sus horizontes al escuchar las opciones de los demás. Lo he hecho en el salón de clases y también con mis hijos y funciona muy bien.

Veamos lo que pasaría dando el número 12:

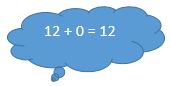6 + 6, 7 + 5 y las demás combinaciones de sumas… que se acaban pronto.

También están las combinaciones de restas, como 13-1, 14-2… y esas son ilimitadas. Interesante, ¿verdad?

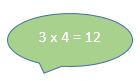Como multiplicación, las combinaciones son pocas: 3 x 4, 2 x 6 y 1 x 12 y con los números en el orden inverso.

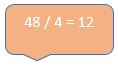Pero como división, nuevamente las combinaciones son ilimitadas: 12 entre 1, 24 entre 2…

Por cierto, me agrada cuando usan el 1 en multiplicaciones y divisiones y el 0 en sumas y restas, porque esa comprensión les ayuda mucho al llegar a ecuaciones.

.
La creatividad y los conocimientos previos pueden llevar a los alumnos a usar más de dos números y más de una operación; a usar fracciones, decimales, raíces y potencias: 12 también es 2 al cuadrado por 3.

.
La actividad sólo toma unos minutos, engancha a los alumnos, los pone en “modo matemático”, desarrolla su sentido numérico y, además, bien manejada es divertida.
Como mamá también lo he hecho con mis hijos. Cada uno ofrece varias opciones de forma intercalada. Incluso con un solo hijo puede hacerse con una opción él y una opción nosotros.

.
Se pueden elegir distintos números que llevan a distintos descubrimientos, como números primos, números que son potencias de otros, números racionales…

Para cerrar

La estrategia empleada para resolver los ejercicios asignados, ya sea en una tarea o en un examen, tiene una influencia importante para que el alumno la realice bien y en el tiempo asignado. Por lo tanto, como profesores y papás debemos buscar que nuestros alumnos e hijos conozcan y dominen esas estrategias para que elijan la mejor. Identificar que hay distintas formas de realizar un cálculo y que algunas funcionan mejor que otras bajo ciertas circunstancias es una buena forma de comenzar.

.
Agradezco de antemano que me escriban sus comentarios y me compartan sus experiencias y sus dudas. Bajo el título de cada entrada se encuentra la opción «comentarios», donde pueden hacerlo.

Rebeca

PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.

PD2: Quiero agradecer a estas dos páginas en las que me apoyo constantemente para redactar el blog: https://pixabay.com/ http://webresizer.com/

Realicé algunas imágenes en Word.