En la entrada pasada (ver aquí) vimos cómo elegir las medidas para crear distintos tipos de triángulos, que sí se pueden construir, con medidas enteras en su altura y sus lados. En esta conoceremos como hacer lo mismo con otras figuras geométricas: algunos cuadriláteros (rombos, romboides, trapecios) y polígonos regulares.

Al ser una continuación de la entrada pasada, los cuidados al enseñar lo que presento esta vez serán similares. Los retomaré aquí para que los tengamos presentes. Recordemos: los perímetros se calculan sumando las longitudes de los lados, lo cual se puede abreviar cuando se tienen varios lados que miden lo mismo. Comenzaremos por entender de dónde salen las fórmulas de áreas.

Paralelogramos

Los paralelogramos son cuadriláteros (figuras de cuatro lados) formados por dos pares de lados paralelos. Cada par de lados paralelos mide lo mismo. Los ángulos opuestos también miden lo mismo y los consecutivos son suplementarios (suman 180 grados).

Como vimos con el cuadrado y el rectángulo, una diagonal divide a todos los paralelogramos en dos triángulos congruentes (con las mismas dimensiones). Además, si trazamos ambas diagonales, éstas se cruzan en su punto medio.

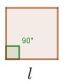El cuadrado es un paralelogramo con todos sus ángulos rectos y todos sus lados iguales.

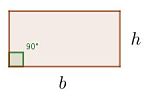El rectángulo es un paralelogramo con todos sus ángulos rectos y sus lados iguales de dos en dos.

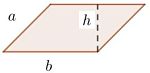El romboide, si se coloca con dos de sus lados horizontales, se ve como un “rectángulo inclinado”. Sus lados son iguales de dos en dos y no tiene ángulos rectos. Tiene la misma fórmula para su área que el rectángulo:

A = b • h.

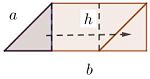Para entender esto, veamos lo que pasa si trazo una línea vertical que “corte” lo que «sobra»sobra de un lado. El triángulo que queda puedo moverlo al otro lado y ahora tengo un rectángulo, con base y altura iguales a las del romboide. Es por ello que todos los paralelogramos, con ángulos rectos o no, comparten fórmula de área:

A = b • h.

Ojo: en un romboide, la altura no tiene la misma medida que el lado inclinado.
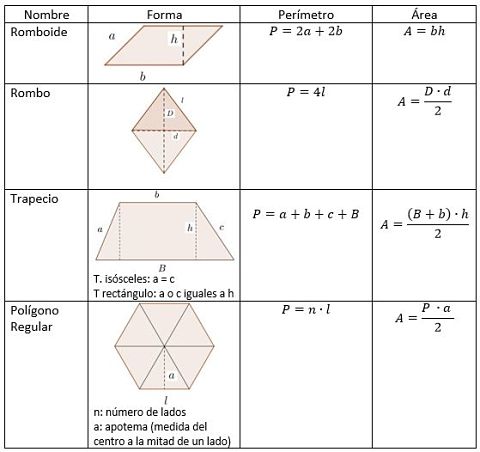
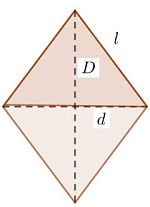El último paralelogramo es el rombo, con todos sus lados iguales y ningún ángulo recto. Si lo acostamos sobre un lado, sería un caso especial de romboide con todos los lados iguales, pero es más común verlo con su diagonal mayor vertical u horizontal. En esa posición se entiende muy bien el porqué de la segunda fórmula (la más conocida) de su área: La diagonal horizontal (d en esta imagen) hace las veces de base de dos triángulos, uno con la punta hacia arriba y otro con la punta hacia abajo. La diagonal mayor (D en esta imagen) es la suma de las alturas de los dos triángulos, por lo que el área sumada de los dos triángulos es:

A = D • d / 2

Trapecios

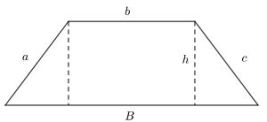El trapecio tiene dos lados paralelos y dos que no lo son. Si los lados que no son paralelos son iguales, se llama trapecio isósceles, y a = c. Si tiene dos ángulos rectos, se llama trapecio rectángulo, y a o c son iguales a h, los demás son trapecios escalenos. La fórmula del área no cambia en los distintos tipos de trapecio.

Para entender el origen de la fórmula veamos que podemos duplicar el trapecio, voltearlo y ponerlo a un lado, con lo que tendremos un romboide cuya base es la suma de las dos bases del trapecio (base mayor y base menor), y cuya altura es la misma que la del trapecio. Por eso el área del trapecio es la mitad del área del paralelogramo formado por los dos trapecios juntos:

A = (B + b) • h /2.

Ojo, el paréntesis indica que es necesario sumar las dos bases antes de multiplicar y dividir, para que el cálculo se haga bien.

Existen más tipos de cuadriláteros, los cuales no tienen fórmulas definidas para sus áreas. Deben “partirse” en figuras más pequeñas para las que sí haya fórmulas, sacar el área de cada una de ellas y sumarlas, por lo que no lo veremos en esta entrada.

Polígonos regulares

Los polígonos regulares son figuras geométricas en las que todos los lados y todos los ángulos son iguales. El triángulo equilátero y el cuadrado son polígonos regulares de 3 y 4 lados respectivamente y ya vimos cómo obtener sus áreas en la entrada pasada. Ahora veremos cómo obtener el área de cualquier otro polígono regular.

Observemos el triángulo verde dentro del hexágono,y veremos que

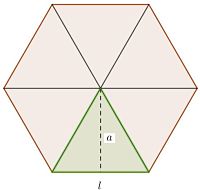El hexágono (seis lados) está formado por… seis triángulos
La base del triángulo es igual al lado del hexágono
El área de un solo triángulo es b • h / 2:
El área de los seis triángulos es igual a seis veces la base de cada uno (o el lado del hexágono) por la altura del triángulo (que es una línea que se llama apotema en el hexágono), entre dos.
El perímetro del hexágono es igual al número de lados multiplicado por la medida del lado.
Si unimos todo lo anterior, entenderemos que:

El área de cualquier polígono regular es igual a la suma de las áreas de los triángulos que lo conforman. Esa suma de áreas se puede calcular directamente como perímetro por apotema sobre dos:

A = P • a / 2

Ojo: es muy importante identificar de dónde a dónde se mide la apotema, ya que la distancia del centro a la mitad del lado es diferente a la del centro al vértice:

Ya que estamos hablando del hexágono, podemos mencionar un dato cultural  interesante. Nos han dicho muchas veces que las matemáticas están por todas partes en la naturaleza, lo cual es cierto. Además es cierto (y creo que se menciona menos) que la naturaleza es muy sabia y le gusta usar sus recursos de forma eficiente. Si se busca matemáticamente cuál es la figura geométrica que puede rodear más área con el menor perímetro, el resultado es: el hexágono.

Esa es la razón por la que las abejas hacen sus panales de forma hexagonal, así pueden guardar la mayor cantidad de miel con usando la menor cantidad de cera. Esta imagen no alude a lo circular de los hot cakes, sino a lo hexagonal del panal donde se elaboró la miel que los cubre.

Volviendo a geometría, en la entrada pasada mencioné que, como profesores, es importante que expliquemos primero de dónde salen las fórmulas y, posteriormente, demos un formulario a los alumnos. También repito aquí que es importante que, en el formulario, se indique claramente qué medida representa cada letra de la fórmula y que se evite el que una misma letra de la fórmula pueda tener distintos valores en la figura.

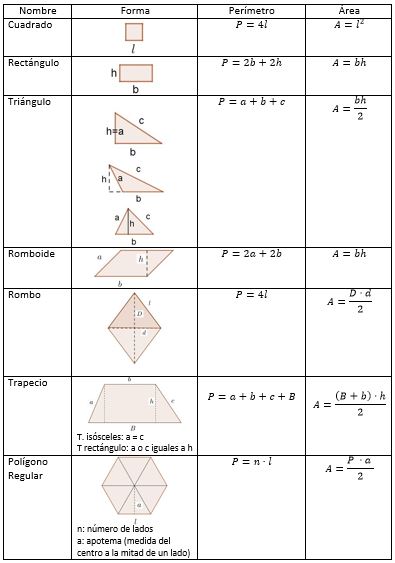
Así queda un formulario de los perímetros y áreas de figuras de esta entrada:

Al final de esta entrada pueden encontrar este formulario unido al de la entrada anterior.

Ternas pitagóricas en la construcción de paralelogramos con medidas enteras

Como también mencioné en la entrada pasada, es importante que el profesor plantee ejercicios con medidas que sean proporcionales dentro de las figuras a las que pertenecen. Para facilitar hacerlo con medidas enteras, en los triángulos, paralelogramos  y trapecios podemos aprovechar las ternas pitagóricas, que son conjuntos de 3 números que cumplen en Teorema de Pitágoras (ver cómo obtenerlas aquí). Estas son las cinco ternas pitagóricas con los valores más pequeños:

(3, 4, 5)    (5, 12, 13)     (7, 24, 25)     (8, 15, 17)     (9, 40, 41)

Veamos ahora cómo usarlas para construir paralelogramos con medidas enteras:

Si a un rectángulo, cuya altura tenga el valor de uno de los números pequeños de una terna pitagórica,  le agregamos dos triángulos rectángulos idénticos, en posiciones invertidas (arriba y abajo) a los extremos, obtenemos un romboide. Veamos cómo se vería con un rectángulo de 6 unidades de base por 4 unidades de altura si le agregamos un triángulo rectángulo con las medidas 3, 4 y 5:

Para construir un rombo con medidas enteras, tomamos cualquier terna pitagórica y dibujamos 4 triángulos rectángulos con los catetos iguales contiguos. Así se vería con el triángulo de 3, 4 y 5:

Ternas pitagóricas en la construcción de trapecios con medidas enteras

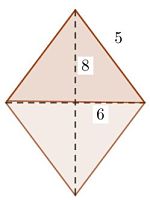
Si a un rectángulo, cuya altura tenga el valor de uno de los números pequeños de una terna pitagórica,  le agregamos dos triángulos rectángulos idénticos, en posiciones invertidas (izquierda y derecha) a los extremos, obtenemos un trapecio isósceles. Veamos cómo se vería con un rectángulo de 6 unidades de base por 4 unidades de altura si le agregamos un triángulo rectángulo con las medidas 3, 4 y 5 a cada lado:

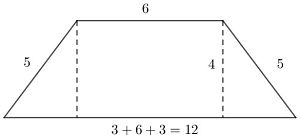
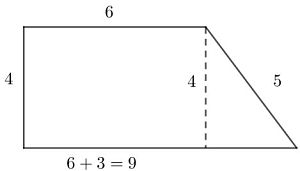
Si a un rectángulo, cuya altura tenga el valor de uno de los números pequeños de una terna pitagórica,  le agregamos un triángulo rectángulo en un extremo, obtenemos un trapecio rectángulo. Veamos cómo se vería con un rectángulo de 6 unidades de base por 4 unidades de altura si le agregamos un triángulo rectángulo con las medidas 3, 4 y 5 a cada lado:

Si a un rectángulo, cuya altura tenga el valor de uno de los números pequeños de dos ternas pitagóricas distintas (pueden ser ternas primarias o múltiplos de las primarias),  le agregamos un triángulo rectángulo distinto a cada extremo, obtenemos un trapecio escaleno. Veamos cómo se vería con un rectángulo de 16 unidades de base por 12 unidades de altura si le agregamos un triángulo rectángulo con las medidas 5, 12 y 13 de un lado y un triángulo de 9, 12 y 15 (el triple de la terna 3, 4 y 5) al otro lado:

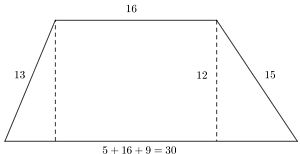
Polígonos con medidas casi enteras

Para polígonos regulares, al menos hasta el dodecágono y hasta 20 unidades de lado, las ternas pitagóricas no sirven para diseñar polígonos que se puedan construir. Por lo tanto, usé una hoja de cálculo y trigonometría para determinar las combinaciones posibles de número de lados y medidas de los lados enteros con los que las apotemas son prácticamente enteras. Aquí está la tabla, en la que n es el número de lados del polígono, l la longitud del lado y a la longitud de la apotema.

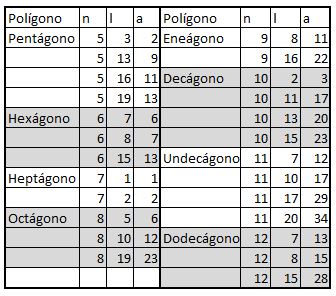
(Nota: la longitud real de la apotema de cada polígono es mayor o menor a la que está en la tabla por menos de un décimo de unidad, por lo que en una construcción con lápiz y papel, o incluso con computadora, prácticamente no se notaría):

Aquí hay unos ejemplos de polígonos de 6, 9, 11 y 12 lados respectivamente, construidos con esas combinaciones de medidas.

Nota: las medidas dentro de cada dibujo están proporcionadas, pero de un dibujo a otro no, debido al editor de imágenes.

Siguiendo las sugerencias de las dos secciones anteriores, los valores principales (lados, alturas y apotemas) y los perímetros serán enteros, y, si elegimos combinaciones que siempre incluyan un número par, también las áreas serán enteras, lo cual facilita que el alumno se concentre en entender los conceptos y procesos de área y perímetro. Ya que los domine puede comenzar a trabajar con números fraccionarios y decimales.

Paréntesis trigonométrico

Si quieren saber cómo replicar o ampliar la tabla de lados y apotemas, pueden leer el siguiente procedimiento. Si no, puede brincarse hasta el siguiente apartado.

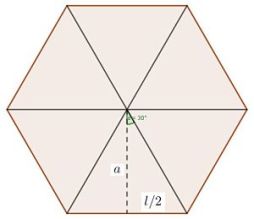
Se usa el número de lados (n) del polígono para determinar el ángulo α (α = π/n). Con ese ángulo y la medida de medio lado se determina el valor de la apotema usando.

apotema = medio lado / tangente del angulo.

Lo anterior es es el despeje de la expresión con la que se calcula la tangente del ángulo: cateto opuesto (medio lado) entre cateto adyacente (apotema). En el dibujo el ángulo aparece en grados, pero en la hoja de cálculo se requiere el dato en radianes:

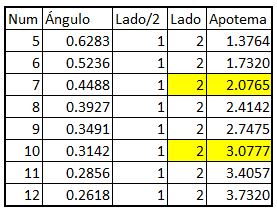
Se hacen los cálculos para las opciones de número y medidas de lados que se quieran analizar y después se eligen aquellos valores de apotema que tengan la precisión deseada. Para hacer la tabla que presenté más arriba, elegí una precisión en que la parte decimal de la apotema fuera menor a 0.1 unidades (opciones marcadas en amarillo), es decir, que la medida fuera prácticamente entera.

Aquí termina el paréntesis trigonométrico.

Para cerrar

Si queremos que nuestros alumnos e hijos enfrenten al mundo con un pensamiento lógico que les permita saber si algo tiene sentido o no (ver más aquí), necesitamos plantearles situaciones y ejercicios que no atenten contra la lógica. En geometría, eso significa proponerles figuras que sean proporcionales en las medidas que les asignamos y que se puedan realmente construir con dichas medidas.

Como mencioné en la entrada pasada, una vez que diseñaron una figura que sí se puede construir, pueden, para dar variedad, multiplicar todos los valores por un mismo número y obtendrán otra que también se puede construir. También pueden cambiar las unidades o voltear la imagen de derecha a izquierda… usen su imaginación para darle más oportunidades de aprendizaje a sus alumnos.

Aquí está el formulario completo con lo que vimos en la entrada pasada y esta:

Como siempre, gracias por leer y compartir. Si quedó alguna duda, escríbanme, por favor. Contestaré.

Rebeca

PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.

PD2: Quiero agradecer a estas dos páginas en las que me apoyo constantemente para redactar el blog: https://pixabay.com/   http://webresizer.com/ y a Geogebra, Excel y Word, que usé para los dibujos, tablas y ecuaciones.