Ésta es la entrada número dieciocho de este blog. Dieciocho es dos veces nueve, que es un número que me encanta (ver sus características en la novena entrada, aquí), así que corresponde hacer algo especial.
 Hoy compartiré algunas ideas que pueden ayudar a desarrollar el pensamiento lógico matemático en personas de todas las edades. Expliqué en la segunda entrada del blog (ver aquí) que lo considero el primer pilar de una buena relación con las matemáticas y que, para mí, el segundo pilar es el sentido numérico (ver aquí).
Hoy compartiré algunas ideas que pueden ayudar a desarrollar el pensamiento lógico matemático en personas de todas las edades. Expliqué en la segunda entrada del blog (ver aquí) que lo considero el primer pilar de una buena relación con las matemáticas y que, para mí, el segundo pilar es el sentido numérico (ver aquí).
Como no es posible desarrollar el pensamiento lógico matemático en algunas clases sueltas a lo largo del ciclo escolar, porque sería un aprendizaje raro, descontextualizado y poco duradero, necesita trabajarse un poco en cada clase o en cada interacción con nuestros hijos. Revisemos algunas ideas para hacerlo y veamos cómo es útil más allá de las actividades escolares.
Más herramientas, más capacidad de actuar
En la primera entrada de este blog (ver aquí) mencioné que lo que yo busco con él es proporcionarles a ustedes, los lectores, una serie de herramientas pedagógico-matemáticas para que las usen según la situación lo requiera. Mientras más herramientas posean, mejor se podrán desenvolver al aprender, enseñar y disfrutar las matemáticas.
 Esos conocimientos, esas herramientas, tanto pedagógicas como matemáticas, se van consiguiendo a lo largo de la vida y es importante que, cuando las tengamos enfrente, las hagamos propias y las organicemos y conectemos con lo demás que ya sabemos. David Ausubel le llama aprendizaje significativo. Debemos, por tanto, evitar que los nuevos conocimientos estén aislados de los anteriores, porque eso nos dificultará el recordarlos y complicará el desarrollo del pensamiento lógico matemático, que implica establecer relaciones entre todo lo que conocemos, como menciona Jean Piaget.
Esos conocimientos, esas herramientas, tanto pedagógicas como matemáticas, se van consiguiendo a lo largo de la vida y es importante que, cuando las tengamos enfrente, las hagamos propias y las organicemos y conectemos con lo demás que ya sabemos. David Ausubel le llama aprendizaje significativo. Debemos, por tanto, evitar que los nuevos conocimientos estén aislados de los anteriores, porque eso nos dificultará el recordarlos y complicará el desarrollo del pensamiento lógico matemático, que implica establecer relaciones entre todo lo que conocemos, como menciona Jean Piaget.
Más conocimientos, más capacidad de interpretar
 Si algo parece una naranja, huele como una naranja y sabe a naranja, lo más probable es que pensemos que es… un zapato, ¿no?
Si algo parece una naranja, huele como una naranja y sabe a naranja, lo más probable es que pensemos que es… un zapato, ¿no?
No, lo lógico es que pensemos que es una naranja. Pero para eso necesitamos poseer algunos conocimientos básicos (cómo se ve, cómo huele y cómo sabe una naranja). Mientras más características de una naranja conozcamos, más seguros estaremos de reconocer una cuando la tengamos enfrente.
 Porque si algo sólo sabe a naranja puede ser una gelatina de ese sabor, si algo sólo parece una naranja puede ser una representación de una naranja en plástico y si algo sólo huele como naranja puede ser ¡un aromatizante para el coche!
Porque si algo sólo sabe a naranja puede ser una gelatina de ese sabor, si algo sólo parece una naranja puede ser una representación de una naranja en plástico y si algo sólo huele como naranja puede ser ¡un aromatizante para el coche!
Me gusta cómo explica Ference Marton esto: mientras más aspectos de “algo” conocemos y más relaciones entre esos aspectos entendemos, podemos aprovechar ese “algo” de formas más poderosas.
Dicho de otra forma, más conocimiento nos vuelve más poderosos, camino a ser superhéroes. Claro, para eso necesitamos el pensamiento lógico matemático, que nos ayuda a usar ese conocimiento para comparar, clasificar, ordenar, relacionar y encontrar dependencias causa-efecto. En resumen, nos ayuda encontrarle la lógica a lo que vemos y con ello, resolver situaciones.
Y el ser capaces de resolver más variedad de situaciones nos da más libertad de elegir nuestro futuro. Por eso escribo este blog. Para ustedes y para mí, que también aprendo mucho con la preparación de cada entrada.
Los tres calcetines
 Cuando aún eran pequeños, pero ya sabían contar, solía decir a mis hijos frases como ésta: “pásame tus tres calcetines para ayudarte a ponértelos”. Su reacción solía ser: “mamá, sólo son dos”. Yo: “¿sólo dos, por qué no tres?”. Hijo: “porque sólo tengo dos pies, mira”. Buen conteo e identificación de relación causa-efecto de su parte.
Cuando aún eran pequeños, pero ya sabían contar, solía decir a mis hijos frases como ésta: “pásame tus tres calcetines para ayudarte a ponértelos”. Su reacción solía ser: “mamá, sólo son dos”. Yo: “¿sólo dos, por qué no tres?”. Hijo: “porque sólo tengo dos pies, mira”. Buen conteo e identificación de relación causa-efecto de su parte.
Y así con todo, mis sufridos hijos necesitaban escuchar con atención lo que les decía, porque solía usar frases sin sentido, como esa, para provocar que estuvieran alerta y que no actuaran en automático. Si nuestros hijos y alumnos ya saben de antemano qué les vamos a decir y qué van a contestar o a hacer, se desarrolla menos su pensamiento lógico matemático.
Con los alumnos podemos hacer algo similar, al decirles algo como: «Pedro tiene 5 pesos y se gasta 3, para saber cuánto dinero le quedó vamos a sumar 5 más 3«.
O algo como: «Esta es una ecuación lineal, vamos a encontrar los dos valores de la incógnita que hacen que se cumpla la igualdad».
 Como papá y profesor es muy divertido pensar en frases ilógicas. Como hijo y alumno también es divertido estar esperando el momento en que algo ilógico ocurrirá, para pescarlo y corregirlo. Y todos mejoramos nuestro pensamiento lógico matemático con este juego.
Como papá y profesor es muy divertido pensar en frases ilógicas. Como hijo y alumno también es divertido estar esperando el momento en que algo ilógico ocurrirá, para pescarlo y corregirlo. Y todos mejoramos nuestro pensamiento lógico matemático con este juego.
(Ojo: No se vale excederse. Debe ser divertido, no irónico, ni abusivo, para que mantenga su sentido didáctico)
Un ejemplo en geometría
Proponer algo ilógico es divertido para todos, cuando es intencionado y controlado. Proporcionar ejercicios ilógicos porque no cuidamos su elaboración no es divertido ni educativo y debe evitarse, porque resulta contraproducente.
De hecho, escribí dos entradas sobre cómo diseñar ejercicios de geometría que no fueran ilógicos. Pueden ver la de triángulos aquí y la de cuadriláteros y polígonos regulares aquí.
 Para desarrollar el pensamiento lógico matemático se puede, por ejemplo, proponer intencionadamente un triángulo cuyos lados midan 5, 10 y 20 cm y pedir a los alumnos que piensen si se podría construir o que lo intenten construir. Deben caer en la cuenta de que en cualquier triángulo la suma de cada par de lados debe ser mayor a la medida del otro, si no, no hay forma de que se unan en un triángulo. Aquí se puede aprovechar para pedirles que opinen sobre qué pueden cambiar para que la construcción sea posible. Se abre un abanico de posibilidades: crecer los lados chicos (pero sólo hasta ciertos valores), reducir el grande (también sólo hasta ciertos valores), se pueden modificar para que el triángulo sea isósceles, equilátero o escaleno.
Para desarrollar el pensamiento lógico matemático se puede, por ejemplo, proponer intencionadamente un triángulo cuyos lados midan 5, 10 y 20 cm y pedir a los alumnos que piensen si se podría construir o que lo intenten construir. Deben caer en la cuenta de que en cualquier triángulo la suma de cada par de lados debe ser mayor a la medida del otro, si no, no hay forma de que se unan en un triángulo. Aquí se puede aprovechar para pedirles que opinen sobre qué pueden cambiar para que la construcción sea posible. Se abre un abanico de posibilidades: crecer los lados chicos (pero sólo hasta ciertos valores), reducir el grande (también sólo hasta ciertos valores), se pueden modificar para que el triángulo sea isósceles, equilátero o escaleno.
Proponer calcular el perímetro de un triángulo cuyos lados miden 5, 10 y 20 cm sólo porque no se puso cuidado al diseñar el ejercicio, hace que los alumnos “desconecten” el pensamiento lógico matemático y trabajen sin analizar lo que hacen. Entregarán 35 cm como respuesta y seguirán con el siguiente ejercicio, con la paz que les da el haber contestado “bien” lo que les pedían, pero sin haber avanzado en la comprensión de lo que es físicamente posible y lo que no.
Observación de patrones
El observar lo que ocurre al contestar ciertos ejercicios para buscar patrones permite prever el tipo de respuesta que debemos obtener en nuevos ejercicios y eso nos ayuda a detectar respuestas erróneas.
Cuando escribí sobre las operaciones con fracciones (ver aquí), observamos este patrón:
Al multiplicar una fracción propia por otra propia se obtiene una que es más pequeña que ambas
Al multiplicar una fracción impropia por otra impropia se obtiene una que es más grande que ambas
Al multiplicar una fracción propia por una impropia se obtiene una que tiene un valor intermedio (más grande que la pequeña y más chica que la grande).
Cuando escribí sobre las tablas de multiplicar (ver aquí), también observamos patrones en su comportamiento.
Cualquier oportunidad de observar patrones apoya al desarrollo del pensamiento lógico matemático.
El patrón de los números al cubo
Aquí hay otro patrón interesante. Imaginen que necesitan relacionar un número con su cubo (el número multiplicado por sí mismo 3 veces), o exactamente al revés: un número con su raíz cúbica. Si tenemos todas las opciones, podemos ordenarlas de menor a mayor y listo (eso también es pensamiento lógico matemático). Pero si sólo tenemos algunos cuantos y nos piden que los relacionemos podemos recordar el patrón que podemos observar aquí:
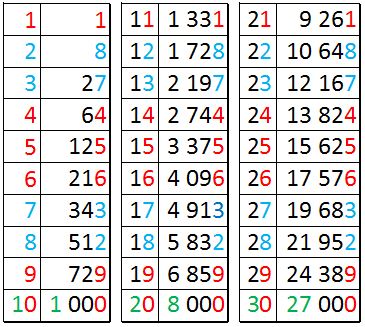
Notarán que para seis de los dígitos en la unidad 1,4,5,6,9,0, el cubo termina en el mismo dígito que el número original. Sólo para 2, 3, 7 y 8 no ocurre, y en esos casos el cubo termina en el dígito que es el complemento a 10 del número original (para el 2 es 8, para el 3 es 7 y viceversa). Los cubos de los números mayores a 10 deben ser mayores a 1000, los mayores a 20 deben ser mayores a 8000 y los mayores a 30 deben ser mayores a 27000 y así sucesivamente (los millares del cubo son el cubo de las decenas del número que se elevó, cuando la unidad es cero).
Con eso podemos decir rápidamente que la raíz cúbica de 4 913 el 17 (4 913 es menor a 8 000), la de 13 824 es 24 (13 824 está entre 8 000 y 27 000, por lo que las decenas son 2) y la de 59 319 es 39 (59 319 es mayor a 27 000 y menor a 64 000, por lo que las decenas son 3). Partiendo de cubos exactos, claro.
Esto se puede convertir en un truco de adivinación: “piensa en un número del 1 al 100, elévalo al cubo con una calculadora, dame el resultado y yo te diré cuál es el número sin calcular la raíz cúbica paso a paso”. No necesitamos sabernos los 100 resultados, sólo recordamos el patrón y listo. Como escribí en la entrada sobre el 9, no es magia, es matemáticas.
Y claro, esto también nos puede facilitar la vida cuando saquemos raíces cúbicas no exactas. Sobre eso escribiré en otra entrada.
Clasificación
Clasificar y explicar la clasificación es básico para desarrollar el pensamiento lógico matemático.
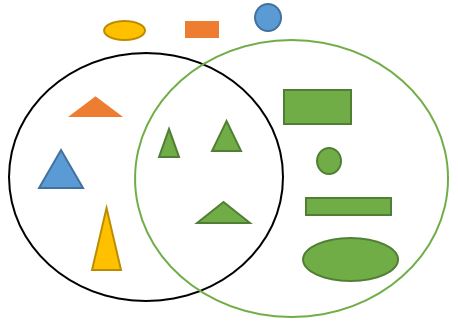
Las figuras geométricas se pueden clasificar por figuras colores, tamaños y combinaciones de ellas: Para las combinaciones se pueden usar lo que se conoce como diagramas de Venn, como éste, en el que todos los triángulos están en un círculo, todo lo verde está en otro y todos los triángulos verdes está en la intersección de los dos círculos. Si hay figuras que no sean ni verdes ni triángulos quedan fuera de esta clasificación.
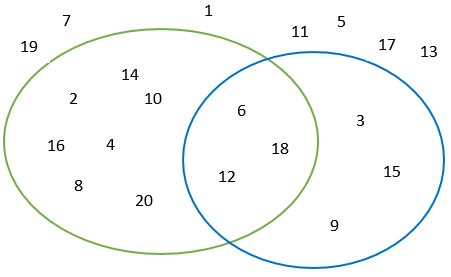
También se pueden clasificar los números según sean múltiplos de otros números. Clasifiquemos los números del 1 al 20 de esta forma: todos los múltiplos de 2 están en un círculo, los de 3 en otro y los que son múltiplos de ambos en la intersección de los dos círculos. Eso refuerza el recordar que los múltiplos de 6 son múltiplos de 2 y de 3 al mismo tiempo.
Todo lo que se va a aprender tiene ciertas características que permiten clasificarlo. Seamos creativos para ayudar a nuestros alumnos a hacer esas clasificaciones antes de empezar a trabajar. Con eso iremos desarrollando poco a poco el pensamiento lógico matemático.
En la vida diaria
Conforme se va desarrollando el pensamiento lógico matemático, la mente se acostumbra a ver algo, conectarlo con todo lo que conoce y a buscar explicaciones a través de esas conexiones. Cada vez con más facilidad y velocidad. A veces tanta, que se siente como que es el instinto el que nos hace saber qué hacer. No sabemos cómo llegamos a la respuesta, pero llegamos (puede que intervengan otros factores, claro, pero yo creo, sin ser experta en el tema, que nuestras experiencias y conocimientos, conscientes e inconscientes, tienen mucho qué ver con lo que nos dicta el instinto).
Eso está bien, sólo hay que tener cuidado al menos en dos sentidos: primero, no dar por hecho que todas las explicaciones que brotaron de nuestro instinto son correctas, porque puede ser que nos haya faltado tomar en cuenta algo por ahí y, segundo, lo que nos dice nuestro instinto puede ser correcto, pero implicar un seguimiento para que se concrete. Si no se da ese seguimiento, puede ser que las cosas al final no salgan como nuestro instinto nos hizo sentir que saldrían.
Me explico con algo no matemático, para variar un poco:
Del primer caso: Vemos a lo lejos a alguien y estamos seguros de que nos vio y no nos saludó. Se nos ocurren una serie de razones por las que no nos saludó y elegimos que está enojado con nosotros, que se volvió descortés o algo aún peor… Conviene asegurarnos de tomar todo en cuenta, lo que puede implicar buscarlo y preguntarle. Nos podría sorprender el saber que ese día olvidó sus lentes y con trabajos veía más allá de un metro, o que estaba angustiado buscando a alguien más y eso lo cegaba de ver cualquier cosa que no se pareciera a quien buscaba. Realmente no tomamos en cuenta todas las posibilidades, por lo que elegimos una incorrecta.
Del segundo caso: Nos enteramos de que darán un curso que nos interesa, resulta accesible y consideramos que nos va a ayudar mucho en nuestro desarrollo personal. Nuestro instinto nos dice que debemos aprovecharlo y nos inscribimos. Sólo que después nos distraemos con otras cosas y no cuidamos el hacer lo necesario para aprovechar los aprendizajes el curso y que eso nos ayude en nuestro desarrollo personal tanto como nuestro instinto nos había dicho que sería, por lo que no logramos tal desarrollo. En este caso no falló nuestro instinto, falló nuestro seguimiento. Siendo conscientes de estos dos cuidados que debemos tener, seguramente lo haremos mejor la siguiente vez.
Sigamos realizando actividades para desarrollar nuestro pensamiento lógico matemático, teniendo los cuidados necesarios para usarlo a nuestro favor.
Antes de irnos
 Se dice que las matemáticas son la ciencia de los patrones. Al volvernos hábiles para identificarlos y crearlos, nos facilitamos mucho nuestro trabajo matemático. Eso nos permite disfrutar más, tanto ese trabajo, como todo lo que observamos en general. Al identificar más detalles, podemos descubrir la belleza menos evidente de las cosas. Yo creo que, en general, se disfruta más lo que se comprende mejor y/o lo que se reconoce que implicó mucho trabajo lograr.
Se dice que las matemáticas son la ciencia de los patrones. Al volvernos hábiles para identificarlos y crearlos, nos facilitamos mucho nuestro trabajo matemático. Eso nos permite disfrutar más, tanto ese trabajo, como todo lo que observamos en general. Al identificar más detalles, podemos descubrir la belleza menos evidente de las cosas. Yo creo que, en general, se disfruta más lo que se comprende mejor y/o lo que se reconoce que implicó mucho trabajo lograr.
Vaya, esta dieciochoava entrada sí que fue especial. Estuvo un poco filosófica e incluso un poco inconexa. Ya retomaremos lo académico en la siguiente.
Como siempre, gracias por leer y compartir con aquellos a quienes consideren que les pueda ser útil lo que aquí publico. Por favor, escríbanme si tienen alguna duda y si quieren sugerirme temas que deseen que aborde en futuras entradas del blog.
Rebeca
PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.
PD2: Quiero agradecer a estas dos páginas en las que me apoyo constantemente para redactar el blog: https://pixabay.com/ http://webresizer.com/
Hice algunas imágenes en Word y Excel
Las ideas de Piaget y Ausubel son muy conocidas, pueden encontrarlas en wikipedia.
Pueden conocer más sobre las ideas de Ference Marton en su libro: Necessary conditions of learning
.



[…] Y me vino a la mente que los colores se «aprenden» en la materia de Matemáticas, principalmente porque identificar y diferenciar los colores nos permite clasificar, que es una habilidad básica del pensamiento lógico matemático, uno de los dos pilares de una buena relación con las matemáticas (ver más sobre pensamiento lógico matemático aquí). […]
Me gustaMe gusta
[…] Clasificar es una de las actividades principales para desarrollar el Pensamiento lógico matemático (ver más aquí y aquí). […]
Me gustaMe gusta
[…] estrategia útil para desarrollar el pensamiento lógico matemático (ver más aquí, aquí y aquí) es hacer preguntas o comentarios absurdos intencionados, del […]
Me gustaMe gusta
[…] y con los patrones y clasificaciones (ver más sobre pensamiento lógico matemático aquí y aquí) y después fomentemos el que usen esas habilidades para explorar libremente y con cierta calma […]
Me gustaMe gusta
[…] de la buena relación con las matemáticas: el pensamiento lógico matemático (ver más aquí y aquí) y el sentido numérico (ver más aquí y […]
Me gustaMe gusta
[…] de una buena relación con las matemáticas, el pensamiento lógico matemático (ver más aquí y aquí} y el sentido numérico (ver más aquí y aquí) sí que son útiles en muchos aspectos de la vida. […]
Me gustaMe gusta
[…] son actividades que permite desarrollar tanto el pensamiento lógico matemático (ver más aquí y aquí) como el sentido numérico (ver más aquí y […]
Me gustaMe gusta
[…] Pensamiento lógico-matemático: útil más allá de lo académico (ver aquí) […]
Me gustaMe gusta
[…] Pensamiento lógico-matemático: útil más allá de lo académico (ver aquí) […]
Me gustaMe gusta
[…] Como quizá habrán deducido, estimar de forma útil puede requerir pensar un poquito más que calcular exacto, así que es un buen ejercicio mental y una habilidad que conviene que desarrollemos en nuestros hijos y alumnos, que les ayudará tanto a trabajar con su sentido numérico (ver más aquí y aquí) como con su pensamiento lógico matemático (ver más aquí y aquí). […]
Me gustaMe gusta
[…] Podemos pedir a nuestros hijos y alumnos que anticipen ciertas características de las respuestas que obtendrán, para que, a la par, desarrollen su pensamiento lógico matemático (ver más aquí y aquí): […]
Me gustaMe gusta
[…] no sólo el sentido numérico, sino también el pensamiento lógico matemático (ver más aquí y aquí). El tiempo invertido en incluirla en las actividades de enseñanza-aprendizaje rendirá grandes […]
Me gustaMe gusta
[…] Cuando tenemos una suma larga de números positivos y negativos, el primer paso que conviene hacer es suprimir paréntesis, para tener claro qué números se sumarán y qué números se restarán. Nota: vean más adelante una forma de proceder observando primero los paréntesis, para reducirlos entre ellos y después suprimir sólo los paréntesis restantes, que es una forma de desarrollar el pensamiento lógico-matemático (ver más aquí y aquí). […]
Me gustaMe gusta
[…] respuestas nos ayuda a desarrollar nuestro pensamiento lógico matemático (ver más aquí y aquí). Tener claro el porqué de cada paso del algoritmo que estamos siguiendo también ayuda en ese […]
Me gustaMe gusta
[…] en los cálculos (ver más aquí y aquí) y fortaleceremos el pensamiento lógico (ver más aquí y aquí), porque es muy probable que algunas de las afirmaciones que se hacen en probabilidad sean […]
Me gustaMe gusta
[…] números que completen las igualdades que observan y su pensamiento lógico (ver más aquí y aquí), al trabajar de forma menos mecánica con las expresiones […]
Me gustaMe gusta
[…] presentes en el calendario. Eso ayuda para desarrollar el pensamiento lógico (ver más aquí, aquí y aquí) y para saber la […]
Me gustaMe gusta
[…] 1111 en el sistema binario. Sin cálculos, sólo usando el pensamiento lógico (ver más aquí y aquí) y los patrones (ver más aquí) que se observan al escribir los números en el sistema […]
Me gustaMe gusta
[…] de las personas con las matemáticas son el pensamiento lógico matemático (ver más aquí y aquí) y el sentido numérico (ver más aquí y aquí). Por ello he escrito esas cuatro entradas y muchas […]
Me gustaMe gusta
[…] y cómo aprovechar sus características para desarrollar el pensamiento lógico (ver más aquí y aquí) y el sentido numérico (ver más aquí y aquí) y, con ello, hacer más eficiente el aprendizaje […]
Me gustaMe gusta
[…] el primer pilar de una buena relación con las matemáticas. En una entrada posterior (la 18, ver aquí) escribí más sobre su utilidad y compartí algunas ideas para […]
Me gustaMe gusta
[…] Recordemos que desarrollar el pensamiento lógico matemático es muy importante también, por lo que es necesario preguntar a los alumnos si les suena lógico que puedan recorrer sólo 5 cuadras para llegar de la casa a la escuela. Me encantaría tener un alumno dijera: si todas las cuadras intermedias son terrenos sin bardas ni vallas, sí. (Ver más sobre pensamiento lógico matemático aquí y aquí). […]
Me gustaMe gusta
[…] adecuadas, podemos desarrollar nuestro pensamiento lógico matemático (ver más aquí y aquí), lo cual nos vuelve más difíciles de manipular y más capaces de aprender ésta y otras […]
Me gustaMe gusta
[…] requiere de usar el sentido común, o el pensamiento lógico-matemático (ver más aquí y aquí) para determinar cómo cambian las cantidades y también para interpretar el resultado. Para esto […]
Me gustaMe gusta
[…] Reconocerlo y actuar en consecuencia ayuda a desarrollar el pensamiento lógico (ver más aquí y aquí) y el sentido numérico (ver más aquí y […]
Me gustaMe gusta
[…] primer pilar es el pensamiento lógico matemático, del que ya he escrito dos entradas (ver aquí y aquí). Ésta será la segunda dedicada específicamente al sentido numérico. También encontrarán […]
Me gustaMe gusta
[…] De una forma similar, podemos obtener la raíz cúbica de un número que sea el cubo exacto de otro número de dos cifras. También se hace con base en los patrones, ahora de los cubos. Pueden ver cómo hacerlo aquí. […]
Me gustaMe gusta
[…] ¿Por qué escribí en el título de esta entrada que los patrones, sucesiones y series nos ayudan a interpretar al mundo? Porque el identificar patrones y usarlos para determinar qué sigue, nos sirve para volvernos hábiles para interpretar lo que ocurre conforme algo avanza y eso es muy útil fuera de la escuela, como lo expliqué en las entradas sobre pensamiento lógico-matemático, que pueden ver aquí y aquí. […]
Me gustaMe gusta
[…] se desarrolla cuando entendemos los por qué (ver más sobre ese pensamiento aquí y aquí). Todo el concepto de este blog se basa en la premisa de entender por […]
Me gustaMe gusta
Me encanta la forma en que nos haces caer en conciencia y además de mostrarnos ejemplos tan próximo como lo que haces con tus hijos para mantenerlos atentos y hacer que usen su lógica, simplemente genial, muchas gracias por todo lo que nos enseñas
Me gustaMe gusta
Gracias por tus palabras, Irma, y por estar dispuesta a aprender ideas para enseñar a tus hijos a usar su lógica, tan necesaria en la vida.
Me gustaMe gusta
Rebeca me la dejaste muy fácil: ya que el número que me das termina en 6, la raíz cúbica también debe terminar en 6 porque es uno de los dígitos que terminan igual y como es mayor que 125 000 menor que 216 000, entoces la raíz cúbica de 175 616 es 56
¿Qué tal, tuve buena maestra?
Me gustaLe gusta a 1 persona
Excelentemente bien contestado, Ericka. ¡Eres una muy buena alumna!
Me gustaMe gusta
Como siempre, súper interesante, vuelves simple lo que parece complicado, gracias por compartir tus estrategias y consejos, ahora sí que me pregunten la raíz cúbica de todos los números 😉
Me gustaLe gusta a 1 persona
Muchas gracias, Ericka, por tus comentarios y por tu entusiasmo para aprender los conceptos y estrategias que comparto y con eso enseñar mejor a tus alumnos.
¿Cuál es la raíz cúbica de 175 616?
¡Saludos!
Me gustaMe gusta