En la entrada pasada (ver aquí) vimos la diferencia entre sucesión, serie y patrón de formación, conocimos algunas formas de iniciar a los niños en las sucesiones y también cómo encontrar un término de una sucesión a partir del patrón de formación. En ésta veremos el proceso inverso, es decir, cómo determinar el patrón de formación de una sucesión de números. Aprovecharemos para ver lo que son las progresiones, así como algunas características de las series.
Empecemos por las progresiones. Como éstas corresponden a las sucesiones más básicas, sus patrones de formación nos ayudarán a entender cómo determinar los de sucesiones más complejas. Recordemos que la n significa el número de término y la a subíndice n significa el término enésimo. Pueden ver ejemplos de cada una un poco más adelante.
Progresiones
Se clasifican, al igual que las sucesiones correspondientes, en:
Aritmética
Su patrón de formación es:
![]()
d es la diferencia (o resta) entre un término y el siguiente de la progresión aritmética. La fórmula indica que un nuevo término es igual al anterior más la diferencia. También puede calcularse como el primer término más n – 1 veces la diferencia. Se le resta 1 a la n porque el primer término no incluye la diferencia.
Geométrica
Su patrón de formación es:
![]()
r es la razón (o división) entre un término y otro de la progresión geométrica. La fórmula indica que un nuevo término es igual al anterior por la razón de la progresión. También puede calcularse como el primer término multiplicado por la razón elevada a la potencia n-1. Se le resta 1 a la n porque el primer término no incluye la razón.
Otros patrones de formación básicos
Nos ayudarán a determinar otros más complejos.
Sucesiones aritméticas para pares y nones
Pares
![]()
Corresponde a: 2, 4, 6, 8, 10…
Funciona para los múltiplos de cualquier número, cambiando el 2 por dicho número.
Nones
![]()
Corresponde a: 1, 3, 5, 7, 9…
Sucesiones que cambian de signo
Cuando se eleva -1 a una potencia 0 o par, se obtiene 1, cuando se eleva a una potencia non, se obtiene -1.
Empezando por positivo
![]()
Corresponde a: 1, -1, 1, -1, 1 …
Empezando por negativo
![]()
Corresponde a: -1, 1, -1, 1, -1 …
Estas cuatro expresiones se pueden integrar dentro de patrones de formación más complejos que incluyan cambio de signo, como veremos más adelante.
¿Cómo se determina un patrón de formación?
Depende del comportamiento de la sucesión:
De primer orden
Recordemos el patrón de formación de las sucesiones o progresiones aritméticas, también llamadas polinomiales de primer orden:
![]()
Se necesita conocer el primer término y la diferencia entre los términos. Por ejemplo:
3, 12, 21, 30, 39…
La diferencia entre cualquier par de términos es 9 y el primer término es 3, por lo tanto:
![]()
Siempre es conveniente comprobar. Lo haremos con el quinto término: 9(5) – 6 = 39.
De segundo orden
El patrón de formación de una sucesión polinomial de segundo orden se ve así:
![]()
B y C pueden ser cero, pero A no, para que sea de segundo orden. Veamos cómo determinar los valores de A, B y C a partir de una sucesión.
5, 15, 31, 53, 81…
Se trata de una sucesión de segundo orden porque la primera diferencia entre los términos no es constante, pero la segunda sí:

Hay varios métodos para llegar al patrón de formación, veamos uno que es sencillo y puedo explicarles por qué funciona, lo cual es fundamental en este blog. Necesitamos obtener el término cero de la sucesión, haciendo los cálculos hacia atrás, de esta forma:

Ahora usamos estas equivalencias:
El doble del coeficiente de la n², A, es igual a la segunda diferencia.
2A = 6 → A = 3
La suma de los coeficientes de la n² y la n, A+B, es igual a la primera diferencia de los términos 0 y 1:
A+B = 4 → como ya sabemos que A=3, entonces B=1
El término independiente, C, es igual al término cero: C=1
Por tanto, el patrón de formación es:
![]()
Comprobemos con el quinto término:
3 (5)² + (5) + 1 = 81
En la pequeña sección siguiente explicaré el porqué de las equivalencias. Quien así lo prefiera, puede omitir su lectura:
La segunda derivada del patrón de formación es 2A. Es constante por tratarse de una expresión de segundo grado y corresponde al cambio del cambio, es decir, a la segunda diferencia, que en el ejemplo sería 6.
Por lo tanto, la segunda diferencia de toda la sucesión de segundo orden es igual a 2A, esto es, al doble del coeficiente principal.
Si restamos el valor del patrón de formación sustituido en 1 menos el sustituido en 0 obtenemos:
[ A(1)² + B(1) + C ] – [ A(0)² + B(0) + C ] = A + B
Por lo tanto, la primera diferencia entre los términos 0 y 1 es igual a A + B. Mediante esa expresión podemos obtener B dado que ya conocemos A.
Al sustituir n = 0 en el patrón de formación, el único valor que queda es C.
Por lo tanto, el término cero es igual a C.
Fin de la breve sección explicativa.
Geométrico
El patrón de formación de una progresión o sucesión geométrica se ve así:
![]()
Se necesita conocer el primer término y la razón entre los términos. Si tenemos la sucesión
5, 15, 45, 135, 405…
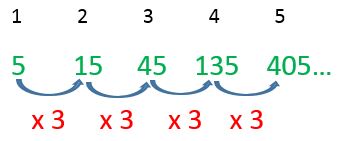
El primer término es 5 y la razón entre cada par de términos consecutivos es 3, por lo que el patrón de formación es:
![]()
Comprobemos con el quinto término:
![]()
Con fracciones
Las sucesiones que involucran fracciones pueden tener patrones de formación muy diferentes. Veamos un par de ejemplos:

Podemos ver que en el numerador está la sucesión de los números nones y en el denominador la de los números pares. Con lo que hemos visto anteriormente, el patrón de formación de la sucesión sería:
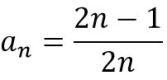
Probemos con el quinto término:
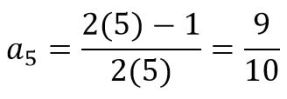
Otro ejemplo:
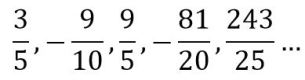
No se identifica a primera vista un patrón, porque el tercer término no sigue de forma evidente la tendencia de los otros. Podemos recurrir a amplificar la fracción, multiplicando numerador y denominador por tres (ver por qué podemos hacerlo aquí), de forma que pueda observarse el patrón, así:
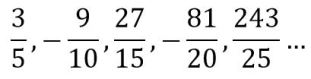
Ahora sí se puede ver claramente lo que ocurre: en el numerador hay una progresión geométrica de potencias de 3, en el denominador están los múltiplos de 5 y los signos van cambiando de un término a otro, empezando por positivo. Uniendo todo lo anterior, el patrón de formación es:
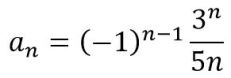
Probemos con el quinto término:

Nota: el numerador se escribiría siguiendo el método que vimos como:
![]()
Pero, por leyes de exponentes, puede también escribirse como

¿Qué podemos preguntar sobre una sucesión?
Como mencioné hace dos entradas (ver aquí) la intención didáctica clara y bien pensada de la pregunta puede llevar a que el alumno logre un mayor aprendizaje al responderla. Veamos las opciones para preguntar que han surgido entre la entrada pasada y ésta, junto con algunas ideas más sobre cómo practicar el tema de sucesiones:
- A partir del patrón de formación, dar el valor de uno o más términos de la sucesión.
- A partir de una sucesión, obtener el patrón de formación.
- A partir de una sucesión, obtener el valor de un término que no se haya dado. Esto implica las dos anteriores, es decir, que obtengan el patrón de formación primero y después el valor del término.
- Dar algunas de las características de la sucesión y algunos de los términos, pero que no sean los primeros y pedir el patrón de formación.
- Dar un patrón de formación o una sucesión para obtenerlo y pedir que determinen si un cierto valor forma parte de la sucesión.
Veamos un ejemplo de la penúltima propuesta:
Si se tiene una sucesión geométrica cuyos términos 6 y 7 son 224 y 448 respectivamente. ¿Cuál es el patrón de formación?
Como sabemos que es geométrica, la razón es constante y la podemos obtener dividiendo ambos términos, ya que son consecutivos. La razón es 448/224 = 2
El patrón de formación de una sucesión geométrica es:
![]()
Conocemos la razón, r, y el valor para el sexto término, por lo que podemos sustituir:
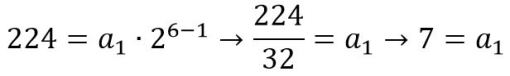
Por lo tanto, el patrón de formación es:
![]()
Comprobamos con el séptimo término, dado que es el que conocemos y no es el que usamos para determinar el patrón de formación:
![]()
Ahora veamos un ejemplo de la última propuesta:
Determina el patrón de formación de la siguiente sucesión, da el valor del décimo término y determina si el valor 81 forma parte de ella:
9, 13, 17, 21, 25…
Podemos ver que la diferencia entre cada par de términos es 4, por lo que es una sucesión polinomial de primer orden, cuyo patrón de formación, dado su primer término y la primera diferencia entre sus términos, es:
![]()
Para calcular el valor del décimo término se sustituye n=10:
![]()
Y para determinar si el valor 81 forma parte de esta sucesión, e incluso saber qué término es, igualamos el patrón de formación a 81 y solucionamos la ecuación para n:
![]()
Por lo tanto, 81 es el término 19 de esta sucesión. Si hubiera salido un número no entero como solución, sabríamos que el valor que analizábamos no forma parte de la sucesión. Por ejemplo, con 82 hubiéramos obtenido 19.25, por lo que 82 no forma parte de la sucesión. Está entre los términos 19 y 20 de ella, por ser de primer orden.
Nota: esta última pregunta sólo debe hacerse si es factible solucionar la ecuación resultante y/o averiguar si el valor es un término de la sucesión calculando una cantidad razonable de términos.
¿Qué otras ideas para practicar con sucesiones se les ocurren? Añadiré otras en la sección de cierre.
¿Cuántos términos se necesitan para determinar el patrón de formación?
Para patrones de formación no muy complejos, que son los acostumbrados en las matemáticas escolares, en teoría con tres términos sería suficiente. Sin embargo, puede no serlo. Les presento aquí un caso de tres términos que admiten al menos dos patrones de formación diferentes, sencillos ambos:
1, 2, 4 puede seguir con:
7, si consideramos una sucesión cuadrática
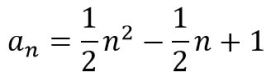
De esta forma:
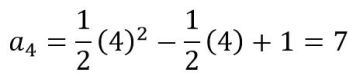
8, si consideramos una sucesión geométrica
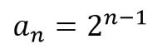
De esta forma:
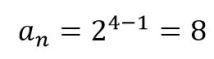
¿Cómo saber cuál es el correcto? Buena pregunta. La mejor respuesta es: necesitamos más datos para estar seguros. Si nos dan el cuarto término ya podemos saber cuál de los dos anteriores es el patrón de formación.
Considero que conviene que el análisis que hagamos vaya de lo sencillo a lo complejo:
El análisis más sencillo es el cálculo de diferencias en uno o dos niveles hasta llegar a la diferencia constante. Si, por el contrario, conocemos que se trata de un ejercicio de sucesiones geométricas, o identificamos que la forma en que crecen los términos es geométrica, entonces ya sabemos que debemos buscar la razón.
Para enriquecer la actividad, podemos preguntar: encuentra al menos dos formas de determinar el término enésimo con base en los primeros tres términos 1, 2, 4, tales que lleven a diferentes números para el cuarto término.
Es importante mencionar que, dados una cierta cantidad de términos, es posible encontrar una patrón de formación que los incluya y, a la vez, incluya cualquier otro que se nos ocurra. A ese patrón de formación se le llama polinomio interpolador y el aprender encontrarlo queda fuera del alcance de esta entrada. Quise mencionarlo porque me parece importante evitar que se queden con la idea de que con los primeros términos de una sucesión se puede determinar uno y sólo un patrón de formación.
Clasificaciones de las series
En esta entrada también vamos a mencionar algunas series. Retomemos las clasificaciones de las sucesiones para interpretarlas como clasificaciones de series. Recordemos que la diferencia entre una sucesión y una serie es que la primera es un listado de números, mientras que la segunda es una suma de números.
Por la forma como varían sus términos
Series aritméticas
La diferencia (resta) entre un término y el siguiente es un valor constante, como en:
1 + 3 + 5 + 7 + …
Series geométricas
la razón (división) entre un término y el siguiente es un valor constante, como en:
2 + 4 + 8 + 16 + …
Por la cantidad de términos
Series finitas
1 + 3 + 5 + 7
Series infinitas
1 + 3 + 5 + 7 + …
Por los resultados de la suma conforme se agregan términos
Series divergentes
La suma crece indefinidamente conforme la cantidad de términos se incrementa
1 + 2 + 3 + 4 + 5 + 6 + … = un valor infinito
Series convergentes
La suma se acerca a un valor conforme la cantidad de términos se incrementa
1 + 1/10 + 1/100 + 1/1000 + … = 10/9
Series telescópicas
Se pueden reducir pares de términos al sumarse
( 1 – 2 ) + ( 2 – 3 ) + ( 3 – 4 ) = – 3
al quitar los paréntesis y reducir los términos sólo quedan los extremos: 1 – 4 = 3.
Los telescopios se pueden expandir o comprimir para enfocar, de ahí el nombre.
¿Cómo se escribe una serie?
Dado un patrón de sucesión, la serie formada por la suma de sus términos se escribe usando la notación sumatoria, o notación sigma, por la legra griega sigma que se usa para ello. Abajo de la sigma se escribe el número de término con el que empieza la suma y arriba el número de término con el que termina. Si es una serie infinita, arriba va el símbolo del infinito.
Así se vería la suma de todos los pares del 2 al infinito:

Y así la suma de los números consecutivos del 1 al 100:
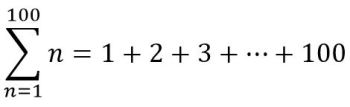
Sobre esta suma en particular, hay una anécdota interesante. Se dice que el profesor de Carl Friedrich Gauss, le pidió que sumara todos los números del 1 al 100, pensando que se estaría un buen rato entretenido en eso. Gauss llegó al resultado casi inmediatamente: 5050. ¿Cómo lo hizo siendo apenas un niño? Se dio cuenta que si sumaba 1+100 + 2 + 99 + 3 + 98 + … + 50 + 51 habría sumado 50 veces 101, con lo cual se obtiene, 5050. Brillante el muchacho, ¿verdad? De hecho, se le conoce como el príncipe de las matemáticas.
Del procedimiento seguido por Gauss se desprende la fórmula para calcular la suma de los números del 1 al n, sin sumar uno por uno.
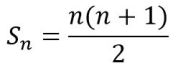
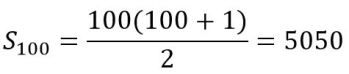
La fórmula funciona aunque los números no sean consecutivos ni empiecen en 1, bajo el mismo principio de sumar los extremos, siempre y cuando la progresión sea aritmética:
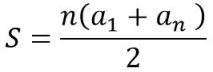
Para cerrar
 Otra serie de circunstancias, similares a las de la semana pasada, complicaron la redacción y entrega temprana de esta entrada. Una disculpa porque tiene poco color. Para compensar un poco, tanto el encabezado como esta sección final están decorados con un colorido patrón.
Otra serie de circunstancias, similares a las de la semana pasada, complicaron la redacción y entrega temprana de esta entrada. Una disculpa porque tiene poco color. Para compensar un poco, tanto el encabezado como esta sección final están decorados con un colorido patrón.
Cierto, falta mostrarles otra forma de aprovechar este tema para que nuestros hijos y alumnos aprendan más. Por ejemplo, se puede extraer más información de las sucesiones aritméticas, según los datos que nos den.
Si nos dan el primer y el último término y, además el número de términos, podemos calcular la diferencia así:
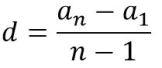
O, si nos dan el primer y el último término y, además, la diferencia, podemos calcular el números de términos así:
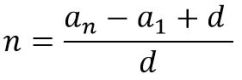
Ambas fórmulas se obtienen despejando el patrón de formación de las sucesiones aritméticas. Dejaremos las opciones con sucesiones de otro tipo para una entrada posterior, porque creo que ésta ya quedó muy larga.
Como siempre, gracias por leer y compartir con aquellos a quienes consideren que les pueda ser útil lo que aquí publico. Por favor, escríbanme si tienen alguna duda y si quieren sugerirme temas que deseen que aborde en futuras entradas del blog.
Rebeca
PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.
PD2: Quiero agradecer a estas dos páginas en las que me apoyo constantemente para redactar el blog: https://pixabay.com/ http://webresizer.com/
Hice algunas imágenes en Word. La historia de Gauss la encuentran en wikipedia.



[…] se llama Sucesiones, series y patrones: nos ayudan a interpretar al mundo. Junto con la siguiente, Sucesiones y series: ¿cómo determinar el patrón de formación?, fueron las primeras escritas a petición de una persona, maestra de educación primaria. ¡Gracias […]
Me gustaMe gusta
Hola, me gustaría saber qué numero de los dos propuestos seguiría esta serie, porque no logro encontrar el patrón: 4, 1, 5, 2, 7…
¿Cómo seguiría, con 3 o con 9? Gracias.
Me gustaMe gusta
Buen día, María,
No se ve claramente el patrón, yo pensaría más bien que fuera un 4, siguiendo un patrón de avanza uno, dos, tres empezando de 4 y luego de 1 de forma intercalada.
Me gustaMe gusta
Realiza un cuadrado de orden 3 y con constante 15 con la siguiente sucesión numérica:
1,2,3,4,5,6,7,8,9
Me gustaLe gusta a 1 persona
Hola, Alejandro,
Supongo que te refieres a armar un «cuadrado mágico» de 3 x 3 casillas (orden 3) que sume 15 (constante 15) en cada fila, cada renglón y cada diagonal. Se puede hacer de varias formas, pero esta es una de ellas:
4 9 2
3 5 7
8 1 6
El 5 va al centro y el resto de los números van por pares que suman 10 en cada sentido alrededor del 5.
¿Me explico?
Me gustaMe gusta
No logro deducir esta serie: 2,13,53,213, … que número sigue y quisiera la explicación
Me gustaLe gusta a 1 persona
Hola, Betsabé, ¿estás segura de que copiaste bien la serie? Porque empezando con 2 no se me ocurre cuál pudiera ser el patrón, pero si empezara con 3 entonces entre el primer y el segundo número habría 10, entre el segundo y el tercero 40, entre el tercero y el cuarto 160 y entre el cuarto y el quinto tendría cierta lógica que hubiera 640, por lo que el quinto número sería 853
Me gustaMe gusta
[…] Eso da pie para recordar que buscar aquello que coincide, aquello que se repite, encontrar patrones, es una importante manera de “hacer matemáticas”, y una de las más útiles. De hecho, las entradas de este blog que han tenido más vistas son las dedicadas a sucesiones, series y patrones (ver más aquí y aquí) […]
Me gustaMe gusta
como eliminar probabilidades matematicamente o buscar la probabildad inversa en juegos de loteria
Me gustaMe gusta
buenas tarde necesito ayuda aqui como resuelvo 40.020;46.202
Me gustaLe gusta a 1 persona
Se necesitan más datos de la sucesión, Ana Doris, o saber el tipo de sucesión.
Si es una sucesión aritmética, el siguiente valor sería 52.384: Se restan 46.202 – 40.020 y eso se le suma a 46.202
Me gustaMe gusta
Buenas me pueden ayudar con una series por favor, debo descubrir el patron de la serie y completar los siguientes numeros
40.000; 20.000; 10.000; _____;______;_____;
Me gustaLe gusta a 1 persona
Buen día, Gaby,
Dados los términos iniciales, el patrón de la serie implica ir dividiendo el número anterior entre 2, a partir del 40 000
Lo que se convierte en este patrón: a_n=80 000/(2^n) o sea 80 000 entre 2 elevado a la potencia n
De esa forma
a_1 = 80 000/(2^1)=40 000
a_2 = 80 000/(2^2)=20 000
a_3 = 80 000/(2^3)=10 000
a_4 = 80 000/(2^4)=5 000
a_5 = 80 000/(2^5)=2 500
a_6 = 80 000/(2^6)=1 250
Saludos
Me gustaLe gusta a 1 persona
Gracias Rebeca Ascencio, Excelente de mucha ayuda..
Me gustaLe gusta a 1 persona
Buenas quien me ayuda con estaeries numericas, me piden descubrir el patron y completar los numeros siguientes?
40000; 20000; 10000;_____;______;_____
Me gustaLe gusta a 1 persona
Hola!, me podría ayudar con la siguiente sucesión por favor: 2, 3, 5, 6, 7, 8, 10… en ella no se cuentan los números naturales al cuadrado, es decir, el 1, 4, 9, 16… y así, llevo un buen rato pero no logro resolverlo, espero me pueda ayudar.
Me gustaLe gusta a 1 persona
Una disculpa, Juan Pablo, estuve investigando un poco y tampoco logré dar con una forma de expresar esa sucesión. Dejaré aquí tu pregunta, por si alguno de los lectores supiera cómo hacerlo.
Saludos.
Me gustaMe gusta
Disculpa, como escribiría en forma de serie: 1-1-1+1+1/2-1/2-1/2+1/2+1/3-1/3-1/3+1/3+…
Me gustaLe gusta a 1 persona
No estoy segura, Nat,
Si fuera directamente 1- 1/2 + 1/3 – 1/4 + … la serie sucesión sería a_n = (-1)^(n+1) * (1/n), con lo cual el signo va cambiando y el denominador va creciendo.
Nunca había visto una serie en la que cuatro términos dependieran de la misma n, me puedes dar más información o algún otro ejemplo, para entender mejor lo que necesitas, por favor.
Me gustaMe gusta
en términos generales estoy buscando una serie condicionalmente convergente cuya serie alternante converge tambien. Te agradecería mucho si supieras de una. se me ocurrió eso pero no se cómo escribirlo pues sería como un reordenamiento, creo.
Me gustaMe gusta
Hasta donde entiendo, las series condicionalmente convergentes suelen ser series alternantes, pues el hecho de que se alternen los signos ayuda a que converjan originalmente, pero no en valor absoluto. Un ejemplo sería el que te compartí (escrito como serie).
Entiendo que los reordenamientos lo que hacen es forzar un resultado, ¿es lo que estás buscando?
Me gustaMe gusta
si rebecca gracias estoy haciendo un taller de matematicas
desde colombia
Me gustaMe gusta
¡Éxito en tu taller!
Saludos desde México
Me gustaMe gusta
hola cual es el patron de :
-1, -3, -7, -13, _ _ _
ayudame rebeca por favor
Me gustaLe gusta a 1 persona
Hola de nuevo, Santiago,
Si sigues el procedimiento que explico en esta entrada, el término 0 también es -1, y los coeficientes del patrón serían: A = -1, B = 1, C = -1.
Entonces el patrón de formación sería:
Con n iniciando en 1 sería a_n = – n^2 + n -1
a_1 = -(1)^2 + 1 – 1 = -1
a_2 = -(2)^2 + 2 – 1 = -3
a_3 = -(3)^2 + 3 – 1 = -7
…
Espero haber podido ayudarte, ánimo
Me gustaMe gusta
cual es el patron de -9, -6, -3, _ _ _
Me gustaLe gusta a 1 persona
Hola de nuevo, Santiago,
Con n iniciando en 1, sería a_n = -12 + 3n
a_1 = -12 + 3(1) = -9
a_2 = -12 + 3(2) = -6
…
Me gustaMe gusta
si la respondiste gracias.
desde colombia
Me gustaMe gusta
hola cual es el patron de +15, +10, +5, _ _ _
Me gustaLe gusta a 1 persona
Hola, Santiago,
Si consideras que n empiece en 1, entonces el patrón de esa sucesión sería a_n = 20 – 5n
a_1 = 20 – 5(1) = 15
a_2 = 20 – 5(2) = 10
…
¿Contesté tu pregunta?
Me gustaMe gusta
Apoyo para encontrar el patron de variacion de los siguientes numeros decimales1.45,1,75 2.05
Me gustaLe gusta a 1 persona
Claro, Francisca:
El valor aumenta de un término de la sucesión al que sigue en 0.30 unidades. El primer término es 1.45, por lo que la sucesión está definida por:
a_n = 1.15 + 0.3n
a_1 = 1.15 + 0.3(1) = 1.45
a_2 = 1.15 + 0.3(2) = 1.75
a_3 = 1.15 + 0.3(3) = 2.02
Espero haberte ayudado.
Rebeca
Me gustaMe gusta
[…] Antes de comenzar, quiero mencionar que, en ocasiones, la llaman serie de Fibonacci, aunque realmente las sucesiones son un listado de números, como en este caso, y las series son una suma de números. Pueden ver más sobre sucesiones, series y patrones aquí y sobre cómo encontrar el patrón de una sucesión o una serie aquí. […]
Me gustaMe gusta
[…] Sucesiones y series: ¿cómo determinar el patrón de formación? (ver aquí) […]
Me gustaMe gusta
Como resuelvo la siguiente sucesiòn,
1,3,6,10,15…etc
¿Es aritmetica o geometrica?
Me gustaMe gusta
Hola, Manuel,
Se trata de una sucesión polinomial de segundo orden, dado que las primeras diferencias entre términos consecutivos son variables: 2,3,4,5 y las segundas diferencias son constantes: 1,1,1…
El patrón de sucesión está dado por: a_n = (n^2) / 2 + n/2, que también se expresa como n(n+1)/2, que es la suma de los números hasta n.
1, 3, 6, 10, 15… son números triangulares, pues pueden acomodarse 1, 3, 6, 10 puntos como un triángulo equilátero (aunque con el uno se necesita usar la imaginación). Si sumas dos números triangulares consecutivos, obtienes un número cuadrado: 1 + 3 = 4, 3 + 6 = 9
Espero haber contestado tu pregunta
Saludos
Rebeca
Me gustaMe gusta
[…] También existen las razones aritméticas y geométricas, que son los incrementos que se dan en las sucesiones. Sobre eso escribí aquí y aquí. […]
Me gustaMe gusta
[…] la de la segunda es aritmética (ver más sobre patrones, series, progresiones y sucesiones aquí y aquí). Todas las tablas serían similares, sólo cambia la base y, por tanto, qué tan rápido […]
Me gustaMe gusta
[…] se suma del 1 al 12 se obtiene: 78 (ver cómo calcularlo como una serie aquí). Al dividirlo entre 3 se obtiene 26. Sólo resta buscar cómo acomodar las líneas para que queden […]
Me gustaMe gusta
[…] entre otras cosas, la comprensión de patrones (ver más sobre series, patrones y sucesiones aquí y aquí) y relaciones entre cantidades y/o expresiones, el lograr la interpretación relacional del signo […]
Me gustaMe gusta
[…] pasa algo similar a lo que ocurre con los conceptos de sucesión, serie y patrón (ver más aquí y aquí). Son conceptos que permiten interpretaciones que pueden resultar muy diferentes. Es decir, en el […]
Me gustaMe gusta
[…] Al primer comportamiento se le llama exponencial y corresponde a una sucesión geométrica que empieza en el (1,2) con un factor 2 al segundo comportamiento se le llama lineal y corresponde a una sucesión aritmética de primer orden que empieza en el (1,2), con d=2 (ver más sobre sucesiones aquí y aquí). […]
Me gustaMe gusta