Estamos ante un problema escrito y descubrimos que contamos con tres datos numéricos y un cuarto dato desconocido, que es lo que nos preguntan. ¿Eso por si sólo convierte al problema en uno de regla de tres? No necesariamente, los problemas que pueden resolverse con una regla de tres tienen características especiales. Además, hay de diferentes tipos y cada uno tiene su propia forma de resolverse.

¿Cómo distinguirlos y resolverlos? De eso tratará esta entrada.
Una vez que hemos aprendido a usar una regla de tres, con sus sencillas operaciones cruzadas, podemos querer emplearla a la menor oportunidad y bajo cualquier circunstancia. Y, si nuestro profesor nos pone en seguida una serie de problemas para los que siempre aplica, probablemente no lleguemos a distinguir bien cuándo realmente es factible resolver el problema así y cuándo no, pues nos podemos limitar a extraer los datos, acomodarlos, hacer los cálculos y dar el resultado, mecánicamente.

Considero que es mejor idea combinar problemas de distintos tipos, al menos de regla de tres directa e inversa, en una misma sesión, para que los alumnos reflexionen sobre las características y eviten contestar de forma mecánica. Para ello, es necesario conocer dichas características. Veamos cuáles son.

Regla de tres directa

En un problema que se resuelve con regla de tres directa, se tienen dos cantidades que están relacionadas de forma directa, esto es, si la cantidad A crece, la cantidad B también crece, y si la cantidad A decrece, la cantidad B también decrece.

Además, cambian en la misma proporción. Si la cantidad A se duplica, la cantidad B también. Si la cantidad A se reduce a la mitad, la cantidad B también. Lo que es constante es el cociente entre los valores (ver la explicación unos párrafos abajo).

Se requiere de usar el sentido común, o el pensamiento lógico-matemático (ver más aquí y aquí) para determinar cómo cambian las cantidades y también para interpretar el resultado. Para esto último, necesitamos un sentido común un poco flexible, porque de repente podremos obtener resultados matemáticamente correctos, pero que no tienen mucha lógica. Veremos un ejemplo de esto último más adelante, primero veamos uno sencillo, resuelto de varias formas distintas.

Deduciendo la respuesta

Si se sabe que para llenar 5 jarrones para flores se requieren 6 litros de agua, ¿cuántos litros de agua se necesitarán para llenar 10 jarrones?

Analicemos la situación: mientras más jarrones haya, más agua se necesita. Y la cantidad de agua aumenta en la misma proporción en la que aumenta la cantidad de jarrones. Por tanto, sí se trata de una regla de tres directa. Si tenemos el doble de jarrones, necesitamos el doble de agua: 12 litros.

Planteando el problema

El problema se puede plantear acomodando la información así:

Observen que las cantidades que corresponden a lo mismo (jarrones/litros) se colocan en la misma columna.

La forma que comúnmente se enseña para resolver una regla de tres directa es multiplicar en la diagonal y dividir en la horizontal, así:

Proporción constante (1)

Ciertos cocientes entre los cuatro datos involucrados en una regla de tres son constantes, y eso se puede observar de dos formas distintas:

Si A (cantidad de jarrones) creció de 5 a 10, la proporción de crecimiento, escrita como cociente, es 10/5 = 2

Para B (cantidad de litros de agua) la proporción de crecimiento debe ser la misma, 2. Eso podemos escribirlo como ?/6 = 2, es decir la cantidad que no conocemos, dividida entre 6, es igual a 2. Multiplicando por 6 a ambos lados del igual obtenemos que la cantidad que no conocíamos es 12.

Como ambas proporciones son iguales, se pueden igualar una a la otra, de esta forma:

Las proporciones son, por tanto, constantes, ya sea que se divida el segundo dato entre el primero, o el primero entre el segundo, de un mismo tipo (jarrones o litros de agua)

10/5 = 12/6

5/10 = 6/12

Pueden ver más sobre operaciones con fracciones aquí y sobre fracciones equivalentes aquí

Proporción constante (2)

La segunda forma en que se puede observar que los cocientes son constantes es al calcular cuánto de B corresponde a una unidad de A, en este caso, cuántos litros de agua se requieren para un sólo jarrón:

Como para 5 jarrones se requieren 6 litros, se requieren 6/5 de litros por jarrón.

Si ahora se tienen 10 jarrones, se multiplica la cantidad necesaria por jarrón, 6/5, por la cantidad de jarrones, 10, para obtener la cantidad de litros: 10 ⋅  6/5 = 12.

Podemos observar cómo los cocientes así expresados también son constantes, es decir, valen lo mismo con el primer par de datos que con el segundo: 6/5 = 12/10

Se podría interpretar también al revés: 5/6 = 10/12  de jarrón se llena con un litro.

Podrán observar que todos los procedimientos llegan al mismo resultado, pues sólo son diferentes formas de entender y resolver el problema.

Recordemos analizar si la respuesta es lógica

Si se necesitan 4 guías para llevar a 48 niños de excursión, ¿cuántos guías se necesitarán para llevar a 87 niños de excursión, manteniendo la misma proporción guías/niños?

Primero analizamos la situación: a más niños, más guías y la proporción se mantiene, por tanto, sí es un problema que se resuelve por regla de tres directa. Acomodamos los datos:

Guías      Niños

4              48

?              87

Y hacemos el cálculo (la incógnita puede estar en cualquiera de las cuatro posiciones, siempre se multiplican los dos datos que sí conocemos que están en diagonal y luego se dividen entre el tercer dato): 87 x 4 / 48 = 7.25

Aquí es donde el sentido común debe entrar en acción y el profesor debe dejar claro a sus alumnos que quiere una respuesta que resuelva el problema, más allá de lo que obtenga en los cálculos.

El alumno podrá ser muy creativo, diciendo que se requieren 7 guías más uno muy chaparrito, o que se requieren 8 guías, algunos de los cuales estarán a cargo de menos niños que los demás, o que se requieren 7 guías y los 3 niños excedentes se irán turnando entre los diferentes grupos o irán con los guías con más experiencia (en caso de presupuesto reducido), etcétera.

Si permitimos a nuestros alumnos realmente resolver problemas, en vez de sólo hacer cálculos, comprenderán mejor para qué están aprendiendo los conceptos y procesos que buscamos enseñarles.

Breve paréntesis algebraico sobre la regla de tres directa

La lectura de esta pequeña sección puede omitirse, es sólo para quien quiera entender por qué se dan las dos igualdades al mismo tiempo y, por tanto, no importa dónde quede la incógnita al acomodar los datos, siempre y cuando en cada columna/fila haya el mismo tipo de dato (niños, jarrones, etc.) y en cada fila/columna se pongan los datos que van juntos (caso 1 y caso 2).

Teniendo la primera igualdad, la que indica que las proporciones en las que aumenta cada valor (A y B) son iguales, podemos multiplicar ambos lados del igual de esta forma para llegar a una segunda igualdad que tiene los valores relacionados de forma distinta (ver más sobre este procedimiento con igualdades aquí).

Y, a partir de esa última igualdad, que indica la proporción constante de A que hay en B, podemos multiplicar nuevamente ambos lados del igual para invertir los valores:

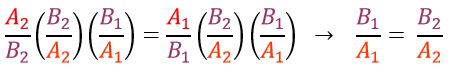
Algo similar podría hacerse con la primera igualdad, la de las proporciones de aumento, para invertir los valores.

Dejando del lado izquierdo del igual cada uno de los cuatro valores, notamos que todos se obtienen siguiendo el proceso de multiplicar y dividir que vimos:

Fin del paréntesis algebraico.

Regla de 3 inversa

En un problema que se resuelve con regla de tres inversa, se tienen dos cantidades que están relacionadas de forma inversa, esto es, si la cantidad A crece, la cantidad B decrece, y si la cantidad A decrece, la cantidad B crece. Además, cambian en una proporción inversa. Si la cantidad A se duplica, la cantidad B se reduce a la mitad. Si la cantidad A se reduce a la mitad, la cantidad B se duplica.

Lo que es constante es el producto de los valores (ver la explicación unos párrafos abajo).

También se requiere el sentido común o el pensamiento lógico-matemático para determinar cómo cambian las cantidades. Y también debemos revisar que los resultados no sólo sean matemáticamente válidos, sino también lógicos fuera de la matemática.

Deduciendo la respuesta

Se tiene una gran bolsa de dulces y se sabe que si se reparte entre 75 niños, a cada uno le tocarán 20 dulces. ¿Cuántos le tocarían a cada niño si hubiera 150 niños?

Analicemos la situación: mientras más niños haya, menos dulces le tocarán a cada niño, por lo que se trata de una regla de tres inversa. Si tenemos el doble de niños, le tocaría a cada uno la mitad de dulces: 10.

Planteando el problema

El problema se puede plantear acomodando la información así:

Observen que las cantidades que corresponden a lo mismo (niños/dulces) se colocan en la misma columna.

La forma que comúnmente se enseña para resolver una regla de tres inversa es multiplicar en horizontal y dividir en vertical, así:

Producto constante

¿Notaron lo que ocurre al hacer la primera multiplicación? Obtenemos el total de dulces de los cuales disponemos: 75 x 20 = 1500. En este tipo de problemas, ese dato es constante, lo que variará será la cantidad de niños y la cantidad de dulces que le toque a cada niño. Al repartir 1500 dulces entre 150 niños, llegamos a los 10 dulces que le tocan a cada niño.

Recordemos analizar si la respuesta es lógica

Si 10 pintores pintan un edificio en 15 días, ¿cuántos pintores se necesitarán para pintar un edificio similar en 3 días?

Reflexionamos que, si se quiere terminar el trabajo en menos días, se requieren más pintores, por lo que se trata de un problema que se resuelve con regla de tres inversa. Acomodamos los datos:

Pintores    Días

   10             15

    ?                3

El dato desconocido también puede estar en cualquier posición en la regla de tres inversa, sólo es necesario cuidar al resolverla multiplicar primero en horizontal y luego dividir en vertical:  ? = 10 x 15 / 3 = 50

Las matemáticas nos dicen que con 50 pintores se acaba de pintar el edificio en 3 días. Pero la lógica nos dice que quizá sea contraproducente tener a tanta gente metida en un edificio y que los tiempos de preparado y secado puede que no permitan hacer el trabajo tan rápido.

Este tipo de problemas conviene plantearlos y evaluarlos con mucho cuidado, para evitar que los alumnos los resuelvan y den respuestas que no sean sensatas, evitando al mismo tiempo suponer que los más pequeños van a tomar en cuenta aspectos sobre los que pueden no tener experiencia, como los tiempos de preparado y secado de la pintura.

Breve paréntesis algebraico sobre la regla de tres inversa

En el caso de la regla de tres inversa, lo que es constante es el producto de los valores de cada caso:

Y las proporciones son inversas (noten que en el lado izquierdo se divide el dato 1 entre el 2 y en el lado derecho se divide al revés, el dato 2 entre el 1):

En el ejemplo de los pintores, si la cantidad de días se divide entre cinco, el número de pintores debe multiplicarse por cinco.

Fin del paréntesis algebraico.

Para cerrar

En esta entrada vimos cómo distinguir los dos tipos de problemas que se resuelven con reglas de tres simples, es decir en las que hay tres datos y es necesario averiguar el cuarto. Es un poco más común encontrar problemas de regla de tres directa, que pueden considerarse problemas de proporción constante, pues se usan valores que crecen/decrecen en la misma proporción. Los problemas de regla de tres inversa, en cambio, pueden considerarse de reparto, pues se reparten dulces, trabajo, etcétera.

Existen, por otro lado, problemas que se resuelven mediante reglas de tres dobles o combinadas. Por cuestiones de espacio, escribiré sobre eso la siguiente semana.

Como siempre, gracias por leer y compartir con aquellos a quienes consideren que les pueda ser útil lo que aquí publico. Confío en que las ideas que comparto en este blog lleguen cada vez a más personas, para que la relación de niños y jóvenes con las matemáticas mejore cada vez más y puedan elegir a que se dedicarán más libremente, sin alejarse de la materia por no entenderla.

Por favor, escríbanme si tienen alguna duda y/o si quieren sugerirme temas que deseen que aborde en futuras entradas.

Rebeca

PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.

PD2: Quiero agradecer a estas dos páginas en las que me apoyo constantemente para redactar el blog: https://pixabay.com/ http://webresizer.com/

Hice algunas imágenes en Word.