Después de conocer el origen del plano cartesiano (ver aquí) y aprender a graficar e interpretar puntos individuales y que siguen un patrón (ver aquí) dedicaremos esta entrada a comprender aquellos aspectos que es necesario cuidar para definir, construir (graficar), interpretar y comparar líneas rectas. 

Antes de empezar, mencionaré que las líneas rectas (también conocidas simplemente como rectas) de las que hablaremos hoy no tienen principio ni final. Son los segmentos de recta los que tienen una longitud limitada, pero no serán tema de esta entrada.

Otro detalle que debemos tener claro es:

Por dos puntos dados pasa una recta y sólo una

Por lo tanto, si tenemos las coordenadas de dos puntos cualquiera que pertenezcan a una recta, podremos definirla. Por cierto, pasa algo parecido con los planos, que explicaré más adelante.

¿Qué distingue a una recta de otra?

Observemos en la imagen las distintas rectas. ¿Cómo les podría yo decir a ustedes en cuál fijarse si todas fueran del mismo color? Necesito encontrar algo que sea característico de cada una y sólo de ella. Ese “algo” es realmente la combinación de dos cosas: cómo es la inclinación de la recta y en qué valor cruza con el eje y (en casos particulares será necesario conocer el cruce con el eje x). Ahora veamos cómo se expresa eso en forma matemática.

¿Qué es la pendiente de una recta?

La pendiente de una recta es su inclinación, como la de la rampa para entrar a ese granero. Tiene una forma muy específica de medirse. Si se toma cualquier par de puntos dentro de la recta y medimos cuánto necesitamos movernos en cada sentido, vertical y horizontal, para llegar de uno a otro, el cociente de esas dos medidas (siempre el cambio vertical entre el cambio horizontal) es la pendiente de la recta. Veamos un ejemplo:

Si queremos saber la pendiente de una recta que pasa por los puntos

(1, 2) y (4, 8) 

podemos notar que, para llegar del primer punto al segundo es necesario avanzar 3 unidades horizontalmente (del 1 al 4) y 6 unidades verticalmente (del 2 al 8). La pendiente en este caso sería 6/3 = 2. A la pendiente de una recta se le suele asignar la letra m, por lo que en este caso, m=2.

Gráficamente se vería así:

Existe una fórmula para hacer esto:

Necesitamos tomar en cuenta esto:

• No importa cuál se tome como primer punto y cuál se tome como segundo, la pendiente obtenida será igual (por dos puntos sólo puede pasar una recta).
• Sí importa evitar mezclar datos. Primero van los del punto que consideramos el segundo (tanto en numerador como en denominador) y luego los del otro.
• El valor de x debe ser diferente en ambos puntos para que la pendiente esté definida
• El valor de y puede ser igual en ambos puntos, en cuyo caso el valor de la pendiente será cero.

En el ejemplo anterior:

Existen cuatro tipos de pendiente, que corresponden a cuatro tipos de rectas. Profundizaremos en eso un poco más adelante.

¿Qué es la ordenada al origen?

Ordenada al origen es un nombre elegante para decir: el valor de y donde la recta cruza el eje de las y. Se le suele asignar la letra b.

Si lo conocemos, lo podemos usar para definir la recta. Si no lo conocemos, lo podemos deducir a partir de otros datos que conozcamos, como veremos más adelante. Si sólo tenemos la gráfica, podemos leerlo de ahí.

Por ejemplo, en esta gráfica la ordenada al origen de la recta azul es b = 0, la de la recta verde es b = 1 y la de la recta roja es b = 3.

Formas de definir una recta mediante una ecuación

Las matemáticas nos ayudan a comunicarnos de manera más clara, precisa y, en ocasiones, abreviada. Las rectas se pueden definir (describir sus características) mediante ecuaciones con distintas estructuras, cada una de las cuales sirve para un objetivo particular.

Una ecuación de una recta es una igualdad que permite calcular, a partir de uno de los valores de la coordenada de cualquier punto de la recta, el otro valor de dicha coordenada. Esto es, si yo tengo la ecuación de una recta y quiero averiguar a qué altura (qué valor de y) está la recta cuando x vale 5, por ejemplo, sólo sustituyo 5 en esa ecuación y calculo el valor de y. Se comprenderá mejor al ver los distintos casos:

Forma «pendiente-ordenada al origen»

Como su imaginativo nombre lo indica, es una ecuación en cuya forma se puede leer directamente la pendiente y la ordenada al origen, ya que se ve así:

Por lo tanto, si sé que la ecuación de una recta es y = -2x + 4, puedo saber, sin hacer ningún cálculo, que se trata de una recta cuya pendiente es m= – 2 y cuya ordenada al origen es b=4.

Es muy importante identificar que el valor de la m siempre acompaña a la x. Es decir, lo que define a la m es el hecho de acompañar a la x, no el hecho de estar después del igual.

Por lo tanto, las rectas y= – 2x + 4  y   y = 4 – 2x son la misma recta, aunque, si queremos ser estrictos, la primera es la que realmente tiene la forma y= mx + b.

Forma punto-pendiente

Otro nombre imaginativo. Es una ecuación en cuya forma se puede leer directamente la pendiente y un punto por el que pasa la recta, ya que se ve así:

Esta forma es muy útil cuando nos dan un ejercicio como este: Determina la ecuación de la recta que pasa por (1, 2) y tiene una pendiente igual a -2.

Al sustituir los datos en la expresión anterior, tenemos:

(y – 2) = -2 ( x -1)  

Que es la misma gráfica del apartado anterior, lo cual podemos comprobar al despejar y: y= – 2x + 4 

Es muy importante cuidar los signos al sustituir, ya que esta fórmula contiene dos signos negativos. Si el valor de alguna de las coordenadas es negativo, lo ponemos entre paréntesis junto al otro signo. La ecuación de la recta que pasa por (-2,-3), con pendiente 4 es:

 ( y – (-3) ) = 4 ( x – (-2) )

Según lo que nos pidan, podemos dejar la expresión en esta forma o llevarla a la anterior, a través de transformaciones algebraicas para despejar la y.

Forma simétrica

En esta forma lo que se ubica a simple vista son las intersecciones con ambos ejes, ya que se ve así.

En esta forma, x e y tienen coeficiente en el numerador igual a 1, a es el valor de la intersección de la recta con el eje x y b es el valor de la intersección de la recta con el eje y (igual que en la primera, lo cual facilita las cosas).

Si nos dan esta ecuación:

podemos identificar fácilmente que se trata de la misma recta de los dos ejemplos anteriores, dadas sus intersecciones con los ejes. Aquí también es necesario cuidar los signos. El que algún valor sea negativo significa que la intersección tiene un valor negativo.

Forma General

Finalmente tenemos la forma general, que se usa cuando se quiere expresar de forma ordenada y con coeficientes enteros una recta, dado que esas son sus características:

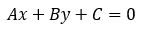
A, B y C son enteros y A es positiva. Esta forma es útil en álgebra lineal, por ejemplo.

2x + y – 4 = 0 sería la forma general de la gráfica que hemos estado analizando.

Comparaciones de rectas

Existen varias formas de clasificar y comparar dos o más rectas entre sí:

Crecientes y decrecientes

Cuando la pendiente es positiva (m>0), se dice que la recta es creciente. También puede entenderse pensando que el valor de y crece cuando el valor de x crece.

Un ejemplo es la primera recta morada: y= 2x, m=2 (no se escribe el valor de b por ser cero). Otro ejemplo es la recta negra: y = x/2 + 3/2,  m = 1/2 . Noten que, mientras menor sea el valor de m, más «acostada» está la recta.

Cuando la pendiente es negativa (m<0), se dice que la recta es decreciente. También puede entenderse pensando que el valor de y decrece cuando el valor de x crece. Un ejemplo es la recta rosa y= – 2x + 4, m= – 2

Observen que lo que indica si la recta es creciente o decreciente es lo que pasa con el valor de y, dado que en ambas descripciones el valor de x crece.

Horizontales y verticales

He mencionado en ocasiones anteriores que conviene cuidar el ser exhaustivos al enseñar. Cuando se analiza la pendiente de una recta, positiva y negativa no son los únicos dos casos. Existen otros dos:

Pendientes iguales a cero (m=0), que se dan cuando el valor de y es constante, es decir, no crece ni decrece al crecer x. Se trata de rectas horizontales, como la verde de la gráfica anterior. Como es horizontal, la x de la expresión se multiplica por cero y no se escribe. Sólo se incluye el valor de b.

y=1 es una recta horizontal que intersecta el eje y en  y=1.

Pendientes indefinidas, que se dan cuando x es constante, como la amarilla de la gráfica anterior, pero  y puede tomar cualquier valor. Se trata de rectas verticales.

x=1 es una recta vertical que intersecta el eje x en x=1.

Sobre las intersecciones con los ejes

Todas las rectas que no son horizontales o verticales intersectan ambos ejes.

Para identificar la intersección con el eje y, se sustituye x=0 (cualquier coordenada sobre el eje y tiene 0 en el valor de x) y se calcula y.

Para identificar la intersección con el eje x, se sustituye y=0 (cualquier coordenada sobre el eje x tiene 0 en el valor de y) y se calcula x.

En cambio, las rectas horizontales pueden estar completamente sobre el eje x (recta x=0) o no tocarlo nunca, y las rectas verticales pueden estar completamente sobre el eje y (recta y=0) o no tocarlo nunca.

Paralelas y perpendiculares

Las rectas paralelas en la geometría euclidiana (está bien, mejor no usemos palabras complicadas: en la geometría que se usa al menos hasta bachillerato) son aquellas que no se tocan por más que se prolonguen en cualquier sentido. Nos enseñan a dibujarlas de forma sencilla apoyando una escuadra en una regla y deslizándola para trazar varias rectas que son paralelas entre sí. Con regla y compás también se puede, sólo que el proceso es más complejo.

Ahora veremos cómo se comparan dos rectas con base en su ecuación, no en su gráfica.

Para llevar a cabo las comparaciones, necesitamos que las ecuaciones estén en la forma: y=mx+b. Es común que en los ejercicios se presenten las ecuaciones en otra forma, para que implique algo de trabajo previo el hacer la comparación.

Una vez en la forma y=mx+b, tenemos dos datos que pueden variar de una recta a otra: m y b:

Cuando m y b son iguales en ambas rectas, se trata de la misma recta (son rectas coincidentes). Inclinación idéntica, intersección eje y idéntica también.

Cuando m es igual para las rectas 1 y 2, pero b  es distinta, se trata de rectas paralelas, porque tienen una inclinación idéntica pero no pasan por el mismo valor de y en el eje y.

Las rectas morada (y = 2x) y roja (y = 2x + 1 ) son paralelas porque las pendientes de ambas son m = 2.

Cuando la pendiente de una de las rectas es el inverso negativo de la pendiente de la otra, sin importar si b es igual o diferente, se trata de rectas perpendiculares:

Las rectas rosa (y = -2x + 4, m = -2) y negra (y = x/2 + 3/2, m=1/2) son perpendiculares, porque una pendiente es -2 y la otra es el inverso negativo de -2, esto es, 1/2.

Cuando la segunda pendiente no es ni igual ni el inverso negativo, se trata de rectas oblicuas.

Es muy importante diferenciar las palabras que son antónimos (significan lo contrario) y las palabras que simplemente no significan lo mismo, pero tampoco forzosamente lo contrario, en el sentido en el que la negación de una signifique la aceptación de la otra. En ese sentido, una recta no horizontal no es forzosamente vertical. Dos rectas no paralelas tampoco son forzosamente perpendiculares, pueden ser oblicuas.

Las líneas rectas que separan los colores de la imagen principal de esta entrada son verticales cada una y paralelas entre sí.

Para cerrar

Cierto, casi olvido explicar lo que pasa con el plano y los puntos. Implica dejar la segunda dimensión y trasladarnos a la tercera…

Por dos puntos en un plano de dos dimensiones pasa una recta y sólo una (dibujen dos puntos e intenten trazar dos rectas distintas que pasen ambas por ellos… no es posible). Y, si dibujamos 3 puntos al azar, necesitamos mucha suerte para que los 3 formen parte de la misma recta, lo más común será que formen parte de 3 rectas distintas, cada una para cada combinación de dos puntos.

De la misma forma, por tres puntos en un espacio de tres dimensiones pasa un plano y sólo uno. Esa es la razón por la que los bancos de 3 patas nunca cojean. No hay forma de que el banco se sostenga en 2 de sus patas y la otra quede volando, siempre tenderá a apoyar las 3 patas en el plano que forma el piso. En cambio, si tengo 4 puntos, no siempre habrá un plano que pase por los 4 a la vez. Esa es la razón por la que los bancos de 4 patas suelen cojear, pues hay que diseñarlos con mucha precisión para que las 4 toquen el piso al mismo tiempo. Si no se diseña bien, se apoyará en dos de sus patas (en diagonal) todo el tiempo e intermitentemente en una de las otras dos, cojeando, lo cual puede ser divertido o molesto, según el humor que tengamos al sentarnos en él.

Claro que si usamos un banco de 3 patas para pararnos sobre él para alcanzar la caja de galletas que «escondimos» sobre el refrigerador, es más probable que pisemos fuera del centro de gravedad y lo desestabilicemos (con la consecuente caída) que con uno de 4 patas. Aunque cojee, un banco de 4 patas es más estable para pararnos en él.

Imaginen el trabajo que le toma a un carpintero lograr que esta mesa de 6 patas toque con todas ellas el piso…

La siguiente vez que estén sentados a una mesa de más de 3 patas que no esté estable… ya saben a qué se debe. Y, si están ante una estable mesa de 3 patas, recuerden no recargarse muy fuerte en una orilla, porque podrían voltearla, lo cual es poco probable que ocurra con una de 4 o más patas. Cada una tiene sus ventajas.

Muchas gracias a los lectores por leer y compartir con aquellos a quienes consideren que les puede resultar útil lo que les comparto. Pueden escribirme para sugerirme abordar algún tema o profundizar en algo sobre lo que ya haya escrito.

Recuerden que escribo algo nuevo cada miércoles. Pueden suscribirse para que les llegue un correo avisándoles cuando la nueva entrada esté lista para leerse.

¡Hasta la próxima semana!

Rebeca

PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.

PD2: Quiero agradecer a estas dos páginas en las que me apoyo constantemente para redactar el blog:  Pixabay   y   Webresizer

Realicé algunas imágenes en Word y en Geogebra