Esta es la entrada 56 de este blog. Coincide con el resultado de la multiplicación que, por algún extraño motivo, resulta más tardada de aprender para los niños: 7 x 8. Como mencioné la semana pasada (ver aquí), dedicaremos esta entrada también a la probabilidad, complementando la anterior.

Veremos cómo calcular las probabilidades condicionadas y las complementarias, así como las uniones y las intersecciones de probabilidades. Aprovecharemos para conocer algunos resultados interesantes relacionados con el tema.

¿Qué tiene qué ver un coche envuelto de regalo con esto de las probabilidades? Sigan leyendo para conocer el problema de Monty Hall y saber cómo elegir para tener más probabilidades de ganar un auto en un programa de concurso.

A propósito del 56, si de las tablas de multiplicar del 1 al 10 hay 100 combinaciones posibles (1 x 1 al 10 x 10), ¿cuál es la probabilidad de que la maestra nos pregunte 7 x 8 en un examen oral?

Si la maestra usa un método de elección de la pregunta basado en el azar y en que las 100 combinaciones tengan la misma probabilidad de ser preguntadas, la probabilidad de que nos pregunte 7 x 8 es de 1/100. Pero si la maestra sólo preguntará aquellas multiplicaciones que sabe que tardan más en aprenderse, la probabilidad de que me la pregunté es mucho más alta y depende de la cantidad de multiplicaciones diferentes que la maestra haya planeado preguntar.

¿Y si mejor usamos algún método mnemotécnico para aprendernos, de una vez por todas, esa multiplicación?

7 x 8 = 56: Siete-ocho -> cinco-seis -> son los dos números anteriores. Pero cuidado, porque 8 x 7 NO es 65. Al multiplicar cualquier número por un par la respuesta debe ser par. Por lo tanto, 7 x 8 = 8 x 7 = 56 (ver más ideas para comprender y memorizar las tablas de multiplicar aquí y aquí)

Vaya, me estoy alejando del tema de hoy. Regresemos a él.

Conceptos que es necesario entender

Algunos ya aparecieron en la entrada pasada:

Eventos favorables: aquellos para los que se calcula la probabilidad de que ocurran.

Eventos posibles: aquellos que tienen alguna probabilidad de ocurrir. Abarcan los favorables y los no favorables.

Eventos mutuamente excluyentes: no pueden ocurrir a la vez. Como cara y cruz al lanzar una moneda. Sólo escribiré sobre este tipo de eventos hoy.

Eventos colectivamente exhaustivos: lista de todos los eventos que pueden ocurrir. No puede ocurrir algo que no esté en esa lista

Probabilidad teórica: eventos favorables / eventos posibles

Probabilidad frecuencial: aciertos / experimentos.

¿Cómo inició el estudio formal de la probabilidad?

Encontré un esbozo de lo que incluyo aquí en el libro Matemáticas I para secundaria de Aldape y Toral.

Se cuenta que el Caballero de la Meré era aficionado a los juegos de azar y le planteó un problema sobre la división de una apuesta a Blais Pascal, quien lo discutió con Pierre Fermat (ambos matemáticos del siglo XVII). El problema en su forma general se expresa así:

Dos personas compiten en un juego hasta completar un cierto número de puntos. Cada una de ellas tiene la misma oportunidad de hacer un punto cada vez. Si se interrumpe el juego antes de que alguno de los jugadores complete los puntos, ¿cómo debe dividirse lo apostado?

Para poderlo entender y responder, es mejor hacerlo a través de un ejemplo, que después se pueda generalizar:

Dos personas (A y B) juegan volados (lanzan una moneda al aire). Si cae cara, A, gana un punto, si cae cruz, B gana un punto. El que complete tres puntos primero gana la apuesta (una cantidad de dinero). Si se interrumpe el juego cuando A lleva dos puntos y B un punto, ¿cómo debe dividirse el dinero de la apuesta?

Veamos las opciones:

Se puede repartir mitad y mitad, pero A no estaría de acuerdo porque llevaba ventaja y debería tocarle más.

Se puede repartir 2/3 del dinero a A y 1/3 a B, para corresponder a la proporción de puntos obtenidos. Esa era la idea del Caballero de la Mére, pero Pascal y Fermat no estaban de acuerdo. ¿Por qué?

Éstas serían todas las posibilidades si se hicieran otros dos tiros. Pueden observar que en tres de las cuatro opciones, A es el que gana. Por lo tanto, la forma más justa de repartir el dinero de la apuesta es tres cuartas partes para A y una cuarta parte para B.

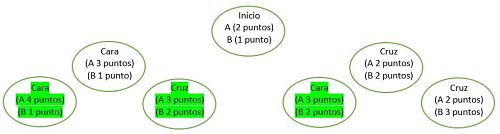
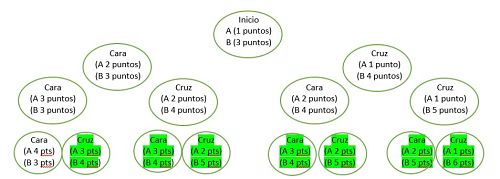
¿Cómo se generalizaría la respuesta al problema? Al igual que se resolvió éste, usando sólo las ramas del árbol de posibles desarrollos que corresponden a la situación desde la que se partió. Por ejemplo, si se parte de que A tenga 1 punto, B tenga 3 puntos y la apuesta la ganaba el que obtuviera 4 puntos, el dinero no debe repartirse una cuarta parte a A y tres cuartas partes a B, según los puntos obtenidos, sino una octava parte a A y siete octavas partes a B, según las probabilidades de ganar que tendrían si siguieran jugando, que pueden verse en esta imagen.

¿Cómo se forma un árbol de posibilidades?

Estas son las posibilidades dados 3 lanzamientos consecutivos de una moneda.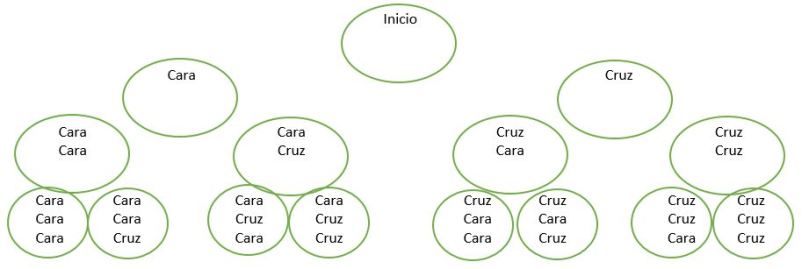

Pueden analizarse de muchas formas:

La probabilidad de 3 caras es de 1/8
La probabilidad de 2 caras (sin importar el orden en que caigan) es de 3/8
La probabilidad de 1 cara (sin importar el orden en que caiga) es de 3/8
La probabilidad de 0 caras es de 1/8
En conjunto, suman 8/8 = 1, dado que son todos los posibles resultados (son los eventos colectivamente exhaustivos que mencionaba al principio).

Pueden observar que cada uno de los 8 casos finales tiene un orden distinto. Por lo tanto, si importa el orden en el que caen las caras y las cruces, tenemos 8 casos distintos, cada uno con una probabilidad de 1/8.

Unión de probabilidades

Si al lanzar una moneda tres veces (o tres monedas una tras otra) queremos calcular la probabilidad de que caigan cara y cruz intercaladas, debemos sumar (unir) la probabilidad de cara-cruz-cara (1/8) más la probabilidad de cruz-cara-cruz (1/8), que son las únicas dos opciones en las que no caen dos lados iguales seguidos. Por tanto, la probabilidad de que tres lanzamientos tengan resultados intercalados es de 1/8 + 1/8 = 1/4.

Intersección de probabilidades

Si se busca calcular la probabilidad de que el primer lanzamiento caiga cara y el segundo caiga cruz, se deben multiplicar las probabilidades: la probabilidad de cara en el primer lanzamiento: 1 / 2, por la probabilidad de cruz en el segundo lanzamiento: 1 / 2, la probabilidad de cara-cruz es 1 / 2 x 1 / 2 = 1 / 4. Si observamos el árbol de posibilidades hasta la rama de dos lanzamientos, veremos que hay cuatro posibilidades: cara-cara, cara-cruz, cruz-cara y cruz-cruz. Sólo 1 de 4 es cara-cruz, lo que es congruente con lo que acabamos de calcular.

Cuando se pueden hacer árboles de posibilidades, es muy sencillo ver y determinar las probabilidades buscadas. Sin embargo, en ocasiones el árbol quedaría demasiado grande e inmanejable, por lo que es necesario hacer los cálculos mediante multiplicaciones y sumas, como las presentadas en estas dos secciones.

Probabilidades complementarias

Son probabilidades que, juntas, completan el 100%. Por ejemplo, en un volado, las probabilidades de cara y de cruz, 50% cada una, son complementarias. Las probabilidades de que caiga cada uno de los números en el lanzamiento de un dado, 1/6 cada una, también lo son. Y la probabilidad de que caiga un número non es complementaria con la probabilidad de que caiga un número par, cuando no hay números que no sean pares o nones en el dado. En el árbol de posibilidades anterior, las probabilidades de 3, 2, 1 y 0 caras son complementarias, dado que suman 8/8.

Cuando las probabilidades son menos sencillas de calcular, debe tenerse cuidado. Por ejemplo, en el caso del Caballero de la Meré, si se calcula la probabilidad de que gane A, 3 / 4, la probabilidad de que gane B debe ser lo que falta para 1, es decir 1 / 4.

Podemos elegir dos estrategias: o calcular ambas probabilidades por separado y comprobar que sumen 1, o calcular la primera probabilidad de la forma acostumbrada y determinar la segunda con sólo restarle a 1 la probabilidad de la primera. Esta segunda estrategia puede ser más rápida, pero tiene una desventaja: si se calcula mal la primera probabilidad, se tendrán mal ambas respuestas. En cambio, con la primera estrategia, la comprobación nos lleva a estar seguros de las respuestas. ¿Qué estrategia seguir?

Depende del tiempo disponible y las implicaciones de tener bien o mal las respuestas. Yo prefiero la primera, para ir a la segura al dar la respuesta, pero entiendo que bajo ciertas circunstancias la segunda puede ser suficiente.

Cálculo de probabilidades con la baraja de póker (francesa)

Veamos algunas probabilidades que se pueden calcular a partir de las cartas de la baraja francesa. Cada carta posee dos características: su palo y su valor. Existen cuatro palos, dos negros: picas y tréboles y dos rojos: diamantes y corazones. Existen 13 valores: los números del 1 al 10 y las 3 figuras identificadas con las letras J, Q, K. Combinados dan 4 x 13 = 52 cartas todas distintas (no consideraremos los comodines).

Cuál es la probabilidad de obtener, al sacar una carta al azar:

El 9 de tréboles: 1/52, dado que sólo hay una carta con esa combinación de palo y valor.

Una carta roja: 26/52 = 1 / 2, dado que 26 de las 52 cartas (la mitad) son rojas.

Un 9 de tréboles o una carta roja: 1/52 + 26/52 = 27/52 Se unen las probabilidades, dado que el 9 de tréboles no es una carta roja (son mutuamente excluyentes).

Una carta que no sea el 9 de tréboles: 1 – 1/52 = 51/52. Es el complemento de la probabilidad de sí sacar el 9 de tréboles, que se puede comprobar sabiendo que hay 51 cartas que no son ésa.

Cuál es la probabilidad de obtener, al sacar una carta, regresarla, mezclar y luego sacar otra (eso significa que, como en los volados de las monedas, las probabilidades no cambian después de sacar la primera carta y regresarla):

La misma carta ambas veces: 1/52 x 1/52 = 1 / 2704

Una carta roja primero y una carta negra después: 1/2 x 1 / 2 = 1 / 4

Dos cartas de distinto color: 1 / 2.

Llegar a esta respuesta requiere de un poco de sentido común, más que de un árbol de posibilidades. La primera carta la mitad de las veces va a salir roja y la mitad de las veces va a salir negra. Lo mismo la segunda, por lo tanto hay cuatro combinaciones, dos con el mismo color (roja-roja, negra-negra) y dos con distinto color (roja-negra, negra-roja). dos de cada cuatro combinaciones son eventos favorables (distinto color), por lo que la probabilidad de obtener dos cartas de distinto color bajo estas circunstancias es 1/2.

¿Y si no se devuelve la carta?

Entonces entramos en una situación completamente distinta, porque las probabilidades cambian de un evento al siguiente, al haber menos cartas cada vez. Lo que sucedió después está condicionado por lo que sucedió antes. Veamos distintos casos.

Probabilidades de una secuencia de cartas, sin devolución

¿Cuál es la probabilidad de que la primera carta sea roja y la segunda sea negra?

26 / 52 x 26 / 51 = 26 / 102

Esto se debe a que al sacar la primera carta, hay 26 rojas y 52 en total. Al sacar la segunda carta hay 26 negras y 51 en total

¿La probabilidad de sacar una carta con el mismo valor y palo? 0

No se devolvió la carta y todas son distintas.

¿La probabilidad de sacar 4 ases al sacar 4 cartas?

4 / 52 x 3 / 51 x 2 / 50 x 1 / 49. Al principio hay 4 ases en 52 cartas, luego quedan 3 ases en 51 cartas, luego 2 en 50 y finalmente 1 en 49. El numerito (sí, es un número muy pequeño) es 1 / 270725.

Considero que entender esta situación condicionada con las cartas nos prepara para comprender dos problemas clásicos de probabilidad:

El problema de Monty Hall

Fue nombrado así en honor del presentador de un programa de concursos llamado “Let’s make a deal”

En el concurso, el participante debe elegir una puerta entre tres, sin conocer qué hay detrás, lo cual será su premio. Lo que puede encontrar es un automóvil en una de las puertas y una cabra en cada una de las otras dos puertas. Una vez que el concursante dice qué puerta eligió, el presentador abre alguna de las otras dos, en las que siempre se encontrará una cabra. Lo que sigue es la parte dramática del concurso: el participante debe elegir si se queda con la puerta que eligió, o la cambia por la otra que no se ha abierto. ¿Tiene las mismas probabilidades de ganar el auto si cambia que si mantiene su elección?

Este es uno de esos casos en los que la respuesta contradice la intuición. Veamos cuál es y cómo entenderla:

La respuesta es: si el participante cambia de puerta tiene 2 / 3 de probabilidades de obtener el coche, si se queda, tiene sólo 1 / 3…

¿Por qué no sería 1 / 2 y 1 / 2?

Porque en un principio tuvo 2 / 3 de probabilidades de escoger una cabra (había 2 cabras en 3 puertas), por lo que cambiar lo lleva al coche. Por otro lado, en un principio tuvo 1 / 3 de probabilidades de escoger el coche (había 1 coche en 3 puertas), por lo que cambiar lo lleva a la cabra oculta. Por tanto, la probabilidad de obtener el coche si cambia es el doble de la probabilidad de obtenerlo si se queda.

Esto podría comprobarse si el concurso se repitiera muchas veces y el concursante siempre cambiara. Por cada dos concursantes que lograran llevarse el coche al cambiar, uno se llevaría una cabra, también al cambiar. Tristemente, no hay forma de saber qué nos tocaría a nosotros en particular si participáramos.

Personas que comparten cumpleaños

¿Cuál es la probabilidad de que dos personas de un mismo grupo de 50 individuos compartan cumpleaños?

Por contra-intuitivo que parezca, en un grupo de 50 individuos es mucho más probable que haya dos personas que compartan cumpleaños a que todos tengan un cumpleaños diferente.

En lo que llevo dando clases me han pasado ambas cosas, dado que suelo tener grupos más pequeños, de 25 o menos personas. Me ha pasado que no haya cumpleaños compartidos, que haya un par de personas con el mismo cumpleaños y otros casos más especiales: dos personas que cumplían ¡el mismo día que yo! En este semestre tengo tres alumnos que cumplen el mismo día, aunque están separados, dos en un grupo y uno en otro.

Revisemos la razón de la afirmación analizando la probabilidad de que dos personas NO compartan cumpleaños (consideraremos que nadie nació en 29 de febrero, para facilitar los cálculos).

Probabilidad de que 2 personas no compartan fecha de cumpleaños:
364/365 -> 99.73%, dado que la segunda tuvo que nacer en cualquiera de los otros 354 días en los que no nació la primera.

Probabilidad de que 3 personas no compartan fecha de cumpleaños:
364/365 x 363/365 -> 99.18%

…

Probabilidad de que 23 personas no compartan fecha de cumpleaños:
364/365 x 363/365 x ….. x 343/365 -> Un poquito menos que 50%

Por tanto, si hay 23 personas en una habitación, hay más de un 50% de probabilidad de que haya dos que compartan cumpleaños. Si hay 57 personas, la probabilidad sube a poco más de 99% y con 366 personas, asumiendo que nadie cumple el 29 de febrero, la probabilidad es del 100% (por el principio del palomar que vimos la semana pasada). Es un buen dato para tener para quien organiza los pasteles de cumpleaños.

¿Cuál es la probabilidad de obtener un par al tirar 5 dados?

Como puede haber muchas combinaciones que den un par, calculemos la probabilidad de que todos los dados den un número distinto:

6/6 x 5/6 x 4/6 x 3/6 x 2/6 -> 9.26%

En el primer dado puede salir cualquier número, en el segundo sólo los 5 números que no han salido, en el tercero sólo los 4 números que no han salido…

Por cierto, la primera fracción no es indispensable escribirla, vale 1 y no afecta el cálculo (no lo hicimos en la sección pasada, en la que los cálculos podían comenzar en 365/365, pero no era necesario escribirlo realmente, al ser 1). Por las características de la probabilidad que se está calculando, el primer dado puede caer en cualquier número y eso es una probabilidad del 100%.

La probabilidad de obtener al menos un par al tirar cinco dados juntos será el complemento de la anterior, es decir 100% – 9.26% = 90.74%

Vaya, sí que es muy alta la probabilidad de obtener un par.

¿Cuál es la probabilidad de obtener un par al sacar 2 cartas?

Es la probabilidad de que la segunda carta tenga el mismo valor que la primera. Quedan 3 cartas con el mismo valor en las 51 cartas restantes, por lo que la probabilidad de que 2 cartas tomadas al azar sea par es de 3/51 -> 5.9% ¡Qué diferencia con respecto a un par en 5 dados!

Para cerrar

Como siempre, gracias por leer y por compartir con aquellos a quienes consideren que les pueda ser útil lo que aquí publico. Es más probable que escriba sobre algún tema que les interese o les sirva si me lo hacen saber a través de un comentario o un mensaje a través de la sección «Contacto». ¡Los espero!

Rebeca

PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.

PD2: Quiero agradecer a estas páginas en las que me apoyo constantemente para redactar el blog: pixabay y webresizer

Hice algunas imágenes en Word (no me quedaron muy bien, pero creo que funcionan)

Tomé algunas ideas del Libro de las Matemáticas, de Cliford A Pickover y de el de Matemática para Iñaki, de Ignacio Zalduendo, así como de Wikipedia como inspiración para escribir esta entrada.