Esta es la entrada 403 de este blog. La escribo un día después de intentar, con las niñas que estoy apoyando, una actividad para comprender las fracciones.

Llevaba dos materiales: unas tiras de plástico rígido que van desde enteros hasta 1/9 y unos círculos de MDF recortados desde la unidad hasta 1/10.

Las exploraron y entendieron que si dice 1/3 es porque se necesitan 3 para formar la unidad, si dice 1/6 se necesitan 6 y así…

También vieron que 1/6 junto con otro 1/6 ocupaban el mismo espacio que 1/3

Luego intentaron armar unidades combinando fracciones distintas. Unir 1/3 + 1/3 + 1/6 + 1/6 estuvo sencillo y correcto.

El problema fue cuando empezaron a combinar varios quintos y séptimos y «parecía» que formaban una unidad, aunque si se hubiera hecho el cálculo matemático se hubieran dado cuenta de que no era así.

Me recordó el chiste en el que una persona le pregunta a otra:

–Si tengo un pastel y lo parto en 3, cada pedazo es el 33.3% del pastel. Entre los tres suman el 99.9% del pastel. ¿Dónde queda el 0.1% restante?

–¡Embarrado en el cuchillo!

(Lo que pasa realmente es que al truncar las cantidades a 33.3% se pierde precisión, si se toman todos los decimales, la suma sí da el 100%)

Así ellas no veían los huequitos que quedaban entre las piezas que estaban comparando.

Lo que haré hoy será llevarles esta imagen, que es un «rompecabezas lógico-geométrico» que llama a cuidar el detalle y los huequitos.

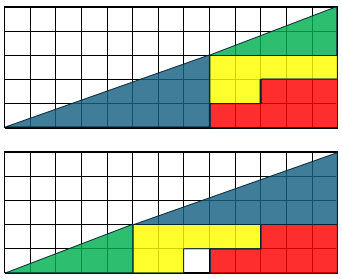
Aunque parece que las piezas en la imagen de arriba cubren una superficie de 5×13/2=32.5 u^2 y las de abajo también, pero con un hueco de una unidad cuadrada, la realidad es que la pieza azul mide 8×3/2=12 u^2, la verde mide 5×2/2=5 u^2, la amarilla 7 u^2 y la roja 8 u^2, esto es, 32 u^2 en total.

Si se usa una regla se podrá observar que la «diagonal» del área de arriba está un poco doblada hacia abajo y por eso el espacio de 32.5 u^2 (si la diagonal fuera recta) se cubre con figuras que sumadas solo miden 32 u^2.

En cambio la «diagonal» del área de abajo está un poco doblada hacia arriba y por eso el espacio de 32.5 u^2 (si la diagonal fuera recta) se cubre con figuras que sumadas solo miden 32 +1 = 33 u^2 .

Hoy intentaré explicar esto a las niñas.

Deséenme suerte.

¡Hasta el próximo miércoles!

PD: Quiero agradecer a esta página en la que me apoyo constantemente para redactar el blog: pixabay.