Esta es la entrada 68 del blog. Cerrará la “trilogía” de entradas relacionadas con los logaritmos, que comenzó con ¿cómo entenderlos y qué cuidados tener al trabajar con ellos? (ver aquí) y siguió con ¿cómo usar las tablas de logaritmos y algunas curiosidades más sobre el tema (ver aquí).
Hoy veremos el tema de las ecuaciones que involucran incógnitas en logaritmos y exponentes. Este tipo de ecuaciones tiene una diferencia importante con respecto a las ecuaciones lineales, cuadráticas, etcétera: pueden resolverse reorganizando la información en una igualdad totalmente nueva e independiente a la anterior, pero igualmente válida. Por eso elegí la imagen que encabeza esta entrada, que representa la reorganización de los elementos de algo para «resolverlo». Sobre las funciones exponenciales y logarítmicas escribiré posteriormente, ya que haya escrito una introducción a funciones en general.
Nuevamente agradezco a Andrés, de Colombia, por haberme sugerido este tema, que resultó muy interesante de construir. Espero que te resulte útil lo que aquí he compartido.
La siguiente semana retomaré los temas de la educación primaria, que son el enfoque principal de este blog. Agradezco de antemano sus sugerencias de temáticas a tratar.Leer más »





 En la segunda entrada de este blog (ver
En la segunda entrada de este blog (ver 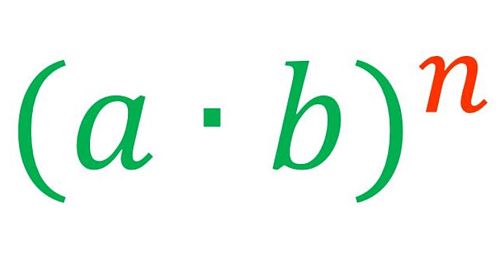
 Conociendo los cuidados que se deben tener según la estructura de la expresión (ver más sobre sentido de estructura
Conociendo los cuidados que se deben tener según la estructura de la expresión (ver más sobre sentido de estructura
 Como en toda la matemática, conviene que los profesores de cualquier grado escolar tengan una idea acerca de los temas futuros en los que se va a usar lo que están enseñando actualmente a sus alumnos. Así podrán, tanto sembrar buenas semillas en ellos, como evitar los atajos que puedan provocarles problemas más adelante. Por ello, esta entrada parte de lo aritmético y llega a lo algebraico.
Como en toda la matemática, conviene que los profesores de cualquier grado escolar tengan una idea acerca de los temas futuros en los que se va a usar lo que están enseñando actualmente a sus alumnos. Así podrán, tanto sembrar buenas semillas en ellos, como evitar los atajos que puedan provocarles problemas más adelante. Por ello, esta entrada parte de lo aritmético y llega a lo algebraico.