Esta es la entrada 204 de este blog.
Mientras pensaba en qué compartirles hoy, me llegó el nuevo video del canal «Derivando», de Eduardo Sáenz de Cabezón, titulado: «El misterioso problema del camello creado de la nada«. Me gustó mucho su enfoque sobre cómo en las matemáticas en ocasiones se requiere usar elementos auxiliares que solo están ahí mientras se resuelve el problema, aunque no forman parte de la solución.
Yo lo muestro en mis clases cuando demuestro el origen de la fórmula general cuadrática (viene en el video) o uso Multiplicadores de Lagrange (los mencionan en el video), pero la idea base del video es un ejemplo genial para entender las aplicaciones de sumas y restas de fracciones, así como la utilidad de conocer sobre múltiplos y divisores.
«Tres hermanos recibieron como herencia 35 camellos. Según la voluntad de su padre, el mayor debía recibir la mitad, el mediano una tercera parte y el pequeño una novena parte de los camellos.»
¿Cómo repartir la herencia dando a cada hermano una cantidad entera de camellos?
Beremiz, el protagonista de «El hombre que calculaba», agrega su camello, hace el reparto y, al final, obtiene su camello de regreso, más un camello extra para su compañero de viaje, dejando a los tres hermanos contentos por haber obtenido más de lo que creían que les tocaba.
¿Cómo pasó eso? Dejo a Eduardo que se los explique en el video.
Al buscar una imagen para ilustrar esta entrada, me surgió la duda (y con ello el título): ¿Cuántas jorobas tiene un camello?
Depende.
Los dromedarios tienen una, los camellos bactrianos dos y los híbridos… una y media.
Pueden leer al respecto aquí.
Hasta el próximo miércoles.
Rebeca
PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.
PD2: Quiero agradecer a estas páginas en las que me apoyo constantemente para redactar el blog: pixabay y webresizer





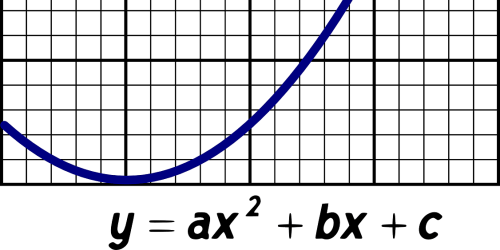


 Comprender a profundidad el significado de este signo comienza por relacionarlo con la igualdad en una balanza y lleva a la igualdad de oportunidades de nuestros hijos y alumnos para elegir carrera, por haber terminado el bachillerato y por sentirse suficientemente hábiles con las matemáticas. Buena razón para escribir sobre él ¿no creen?
Comprender a profundidad el significado de este signo comienza por relacionarlo con la igualdad en una balanza y lleva a la igualdad de oportunidades de nuestros hijos y alumnos para elegir carrera, por haber terminado el bachillerato y por sentirse suficientemente hábiles con las matemáticas. Buena razón para escribir sobre él ¿no creen?
 Por medio de las preguntas que hacemos (ver más sobre preguntas con intención didáctica clara
Por medio de las preguntas que hacemos (ver más sobre preguntas con intención didáctica clara 
 Ya hemos revisado las desigualdades lineales en la entrada 35 (ver
Ya hemos revisado las desigualdades lineales en la entrada 35 (ver 
 Cuando un tema es muy extenso, lo separo en dos o más entradas, que regularmente publico de forma consecutiva. Sin embargo, la situación con el tema de las desigualdades resultó… desigual. Esto se debe a que la primera parte fue la entrada 35 (ver
Cuando un tema es muy extenso, lo separo en dos o más entradas, que regularmente publico de forma consecutiva. Sin embargo, la situación con el tema de las desigualdades resultó… desigual. Esto se debe a que la primera parte fue la entrada 35 (ver