En la entrada pasada (ver aquí) escribí sobre qué es una ecuación, para qué sirve, qué significa resolverla, cuántas soluciones tiene, qué cuidados es necesario tener al resolverla, cuáles son las operaciones con las que se resuelve, por qué es importante entender la solución de ecuaciones de la forma correcta y concluí con una idea para iniciar a los niños de primaria en el álgebra… Vaya, a veces alcanzo a compartir mucha información en una sola entrada. Lo bueno es que ustedes pueden tomarse el tiempo que necesiten para leerla y hacerla suya. La información se queda ahí para cuando requieran consultarla.
Esta entrada es un complemento a la anterior, describo con más detalle algunos conceptos y proporciono más estrategias para solucionar ecuaciones lineales con una incógnita (como un mapa y una brújula para «encontrar el valor de x«). Incluí una sección con ideas para construir ecuaciones lineales con una incógnita que sean interesantes de resolver (digamos que son instrucciones para «esconder el valor de x«).Leer más »
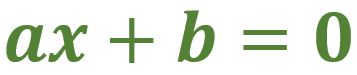
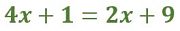Ahora escribiré sobre lo que es una ecuación, lo que significa “resolver una ecuación” y los cuidados que son necesarios al “resolver una ecuación lineal con una incógnita”. También incluiré una sugerencia sobre cómo plantear ejercicios en primaria que preparen a los alumnos para resolver ecuaciones lineales en secundaria.
Un desafío más emocionante es armar objetos con piezas intercambiables. Una misma pieza puede tener distintas funciones según su posición. La relación entre dos piezas puede ser diferente según la forma en que se unan, esto es, según la estructura del objeto.
Las expresiones matemáticas, en especial las algebraicas, también tienen una estructura y están formadas por piezas, o elementos, cuya función es variable y depende de a qué otros elementos están unidos y de qué forma.
IMPULSO MATEMÁTICO 