Ésta es la entrada 54 de este blog. Por ser múltiplo de 9, toca escribir sobre algo especial. He decidido dedicarla al signo igual, esas dos líneas paralelas tan importantes en las matemáticas y cuya correcta comprensión en la primaria (aritmética) facilita muchísimo las cosas en la secundaria (álgebra) y más allá (cálculo diferencial e integral y demás). Si con este blog busco, entre otras cosas, mejorar la relación de las personas con las matemáticas, enfocarnos hoy en algo tan importante para lograrlo es una buena idea.
Comprender a profundidad el significado de este signo comienza por relacionarlo con la igualdad en una balanza y lleva a la igualdad de oportunidades de nuestros hijos y alumnos para elegir carrera, por haber terminado el bachillerato y por sentirse suficientemente hábiles con las matemáticas. Buena razón para escribir sobre él ¿no creen?
Si bien ya había escrito un poco sobre el signo igual en una entrada pasada sobre sentido de estructura (ver aquí) y en dos relacionadas con las ecuaciones lineales (ver aquí y aquí), ésta será una entrada que complemente a aquellas, abordada desde una perspectiva distinta, que incluye ideas para trabajar en primaria para preparar a los alumnos para el álgebra, así como ideas para trabajar en secundaria asegurando la correcta comprensión del significado del signo igual antes de pedir a un alumno que escriba o resuelva una ecuación.
Mi aventura desentrañando las razones de las dificultades matemáticas de las personas me ha llevado a concluir que los profesores de primaria pueden hacer mucho por evitarlas si eligen estrategias didácticas adecuadas, basadas en que ellos mismos comprendan los temas a profundidad y visualicen cómo se conectan con los anteriores y con los siguientes. Apoyarlos en ese sentido es otro de los objetivos de este blog y de esta entrada en particular.Leer más »
En la entrada pasada (ver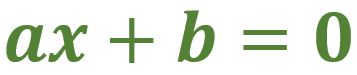 
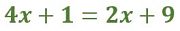Ahora escribiré sobre lo que es una ecuación, lo que significa “resolver una ecuación” y los cuidados que son necesarios al “resolver una ecuación lineal con una incógnita”. También incluiré una sugerencia sobre cómo plantear ejercicios en primaria que preparen a los alumnos para resolver ecuaciones lineales en secundaria.
Un desafío más emocionante es armar objetos con piezas intercambiables. Una misma pieza puede tener distintas funciones según su posición. La relación entre dos piezas puede ser diferente según la forma en que se unan, esto es, según la estructura del objeto.
Las expresiones matemáticas, en especial las algebraicas, también tienen una estructura y están formadas por piezas, o elementos, cuya función es variable y depende de a qué otros elementos están unidos y de qué forma.
IMPULSO MATEMÁTICO 