Esta es la entrada 79 del blog, que es relevante porque se publica exactamente año y medio después de la primera entrada, que vio la luz el 24 de enero de 2018. Buscando ideas para el tema de hoy, pensé en centrarlo en el número uno punto cinco.
¿Qué tanto se puede decir alrededor de este número?
Será una entrada un poco ecléctica, en la que aprovecharemos para puntualizar, entre otros temas, sobre distintas representaciones numéricas. Sigan leyendo para saber lo que se me ocurrió a mí. Compartan en los comentarios lo que se les ocurra a ustedes, por favor.Leer más »
Al resolver cierto tipo de problemas del día a día, un resultado estimado puede ser tanto o más útil que un resultado exacto. Si vamos a comprar pintura para recubrir una pared, saber que necesitamos 5.158 litros para cubrirla puede ser un dato exacto que no es realmente útil, pues en la tienda no nos venderán esa cantidad exactamente, además de que el rendimiento de la pintura es aproximado, por lo que en la realidad es suficiente con estimar que al comprar 5.25 litros (cinco litros más un cuarto de litro) podemos considerar que nos va a alcanzar.
Veremos cómo funcionan las tablas de logaritmos y antilogaritmos, que se han vuelto una curiosidad de museo, dadas la ubicuidad de las calculadoras. Los invito a que disfrutemos esas tablas como se disfruta observar objetos antiguos en un museo y aprovechemos para comprender mejor las propiedades de los logaritmos y las leyes de los exponentes durante el proceso.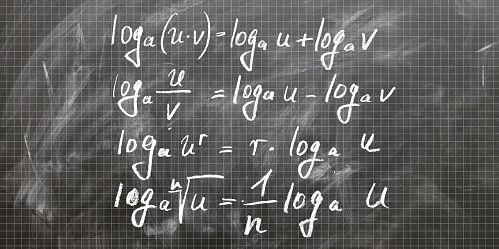
Cuando no existían las calculadoras, tener una tabla de logaritmos era como tener un as bajo la manga, hoy veremos por qué. Pensarán entonces que actualmente ya no tiene sentido estudiarlos… y tendrían razón, si el único uso de los logaritmos fuese hacer cálculos más rápidos. Realmente existen más aplicaciones, algunas de las cuales veremos hoy, con lo que comprenderemos que estudiarlos sí es relevante. La próxima semana complementaré esta entrada con más ideas sobre el tema, así como estrategias para resolver ecuaciones que involucren logaritmos.
Dedicaremos esta entrada a complementar la 62 (ver 
Comprender qué es la reversibilidad en general y en matemáticas en particular facilitará de forma importante el aprendizaje y la enseñanza de la materia, por diversas razones que veremos a lo largo de la entrada.
Ésta es la entrada 62 de este blog. La dedicaremos a las conversiones de las unidades de medida básicas (longitud, área, volumen y masa) en el Sistema Internacional de Unidades. En una entrada posterior complementaremos con conversiones de otras unidades dentro de ese mismo sistema y con conversiones dentro, hacia y desde el Sistema Inglés de Unidades.
Al usar las palabras «negativo/positivo» para buscar imágenes, aparecían personas negativas y positivas, pilas con sus polos negativos y positivos y… sentí mucha nostalgia con las imágenes de los negativos de las fotografías que se usaban cuando yo era niña, así que decidí usar una para ilustrar esta entrada. Una pequeña libertad «poética» que me dí, porque realmente será una entrada dedicada a números y nada más.
Esta es la entrada 60 del blog. Queda bien dedicarla a algo muy relacionado con el número 60: el reloj, con sus 60 minutos en cada hora y sus 60 segundos en cada minuto.
IMPULSO MATEMÁTICO 