Esta es la entrada 426 de este blog. La imagen representa cómo terminé el sábado pasado después del taller para niños con Altas Capacidades.

Trabajar con niños con rezago académico tiene retos enormes: se necesita entender qué conocimientos y habilidades, incluso actitudes, poseen para construir sobre ellos los nuevos conocimientos.

Justo hace unos días intentaba enseñar solución de ecuaciones de primer grado a una muchacha y me di cuenta de que no sabía lo que era calcular el valor de una expresión algebraica (para comprobar su respuesta). Cuando le intentaba enseñar eso me di cuenta de que no conocía la jerarquía de las operaciones matemáticas. Y cuando llegamos a ese punto varias tablas de multiplicar le fallaban también…

Con mucha paciencia fuimos revisando todos esos temas previos para regresar a aquello que estaba viendo en clase.

Hacerlo requiere tener claro los conocimientos prerrequisito y experiencia identificando los faltantes y cómo atenderlos. Requiere esfuerzo y tiempo, pero puede hacerse, de hecho debe hacerse pausadamente.

Trabajar con niños con Altas Capacidades, a quienes el cerebro les funciona a mucha velocidad y entienden con mucha facilidad cómo resolver los retos que se les plantean, es una situación radicalmente distinta.

También se necesitan dominar los andamiajes de los retos que se les quieren poner para poder ubicar en dónde están y cómo llevarlos a través de la aventura de desafiar sus habilidades.

La diferencia es que esto no puede hacerse pausadamente. Esas cabecitas pueden entender y resolver lo que les vayamos planteando de maneras muy rápidas y demandan retos cada vez más complejos porque tienen hambre de ellos.

Y mantener ese ritmo con hasta cinco niños al mismo tiempo durante casi tres horas fue una labor extenuante.

Afortunadamente me tocaron pocos niños que exigían más de manera poco respetuosa, la mayoría solo quería más porque se la estaba pasando bien y querían ver qué más les podía plantear.

Y también afortunadamente el T3RCIA aguantó el esfuerzo. Es un material lógicamente estructurado con el que se pueden hacer muchísimos retos lógicos, y en eso entretuve a los niños.

Porque los retos numéricos los dominaban rapidísimo, pero los retos lógicos sí les representaban un esfuerzo que disfrutaban. Y yo con ellos.

Pueden ver más sobre material lógicamente estructurado aquí, sobre los materiales didácticos que llevé al taller aquí, sobre algunas de las actividades que hice en el taller aquí y aquí.

¡Hasta el siguiente miércoles!

PD: Quiero agradecer a esta página en la que me apoyo constantemente para redactar el blog: pixabay.

Esta es la entrada 420 de este blog. La escribo en medio de una semana en la que sigo abriendo frentes de apoyo a la niñez vulnerable. Hay tanto por hacer…

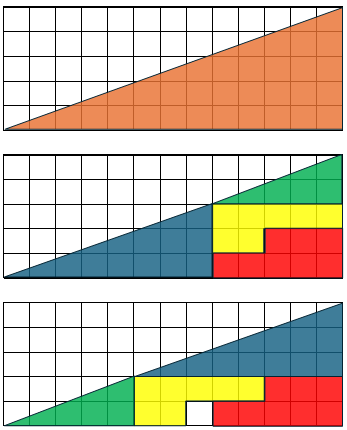
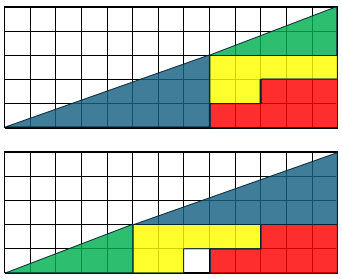
El título de la entrada se refiere a que, si se acomodan las fechas de febrero 2026 en un calendario que tenga los domingos hasta la izquierda, queda un rectángulo de 4 x 7 días, sin ningún día sobrando ni al inicio ni al final, ni ningún hueco (ver imagen de portada). Un mes que se representa de manera compacta, lo cual es algo muy poco frecuente.

La vez pasada que ocurrió fue en 2015 y la siguiente será hasta 2037, aunque eso no significa que ocurra cada 11 años siempre. Antes fue en 1998 y 2009 y después será en 2043 y 2054. Interesante patrón, no creen?

Dado que hay 7 días distintos en los que puede empezar un año y 2 tipos de año distintos (bisiesto o no), hay 14 tipos distintos de calendario y en esos la forma en la que se acomodan los días de un mes se repite 2 a 2 para 11 de los meses.

Excepto para febrero. Cuando no es año bisiesto, como este 2026 y los demás que mencioné antes, el acomodo de días si febrero empieza en domingo es un rectángulo perfecto y compacto que termina en sábado. Pero si fuera año bisiesto, como fue 2004 o será 2032, entonces el mes empezará en domingo pero terminará en domingo y ¡ya no será un rectángulo perfecto y compacto!

Para las culturas en las que el calendario se acomoda con los lunes hasta la izquierda, febrero de 2027 será el siguiente mes rectangular.

Por cierto, 420, el número de la entrada de hoy, es 15 veces 28, los días del mes actual. Mera coincidencia. Y hoy es el día 4 del mes 2, 42, la décima parte del número de la entrada.

Reitero que estos análisis, que podrían tener poca utilidad práctica, tienen una gran utilidad de entrenamiento en búsqueda de patrones. Y eso es muy, muy útil para estructurar el pensamiento

Por cierto, si quieren saber cómo hice este análisis, la explicación general del funcionamiento de los calendarios y el archivo en el que me basé pueden verlos aquí.

Los dejo por hoy, voy a seguir pensando en cómo lograr que la pequeña Génesis distinga y nombre correctamente los cuadrados y los rectángulos.

¡Hasta el siguiente miércoles!

PD: Quiero agradecer a esta página en la que me apoyo constantemente para redactar el blog: pixabay.

Esta es la entrada 419 de este blog. La escribo 4 días después de que se cumplieron ¡8! años escribiendo casi cada miércoles. Y también la semana que decidí reencontrarme con el cubo Rubik por enésima vez en mi vida. Por cierto, 8 es es cubo de 2, hablando de relaciones numéricas interesantes.

Seré hábil para algunas cosas, pero la ubicación y la percepción espacial no son mi fuerte. Antes de que existiera Google Maps y iba para todas partes (incluso dentro de mi ciudad) con un mapa en papel en la guantera. Y los ejercicios de imaginarte un objeto en tercera dimensión a partir de sus caras me costaban mucho esfuerzo y concentración.

Así que mis reiterados intentos de aprender a «resolver» el cubo Rubik no pasaron de una única cara. Cuando mis hijos tuvieron edad me dije que aprendería para enseñarles y… aprendieron antes que yo y lo dejé por la paz nuevamente.

Hasta la semana pasada en la que le regalé a una niña del internado al que apoyo uno y le dije que «competiríamos» para ver quién aprende a resolverlo completo.

El fin de semana le dediqué algunos momentos a revisar tutoriales en YouTube. Descubrí lo siguiente:

-La nomenclatura de los movimientos es relativamente universal y es necesario practicarla mucho para que salga en automático usando un par de dedos nada más.

-Los algoritmos cambian dependiendo de a quién le preguntes. Entiendo que hay unos más eficientes que otros, pero…

-TODOS los tutoriales que he encontrado en YouTube se centran en decirte cómo resolverlo lo más rápidamente posible, aunque yo lo que quiero es ¡entender! cómo funciona… ¿por qué cuando hago cierto algoritmo una esquina se reacomoda «mágicamente»?

-Porque yo no funciono siguiendo algoritmos, mi mente ansía saber el «por qué» de todo (es la brújula que siempre ha guiado este blog, explicar los por qué de los procedimientos matemáticos que se enseñan en la escuela).

-Necesito ponerme a averiguar por mí misma esos por qué, pero es tan hipnótico el moverle y que todo se «desacomode» que… me está costando. Al final de cada día le pido a mi hija que me lo arme y al día siguiente reintento entender la lógica de qué se va para dónde cuando se hace qué combinación de movimientos.

Recuerden: no me interesa aprender a resolverlo rápido, me interesa aprender a resolverlo entendiendo lo que estoy haciendo. Y creo que la niña del internado es de las mías, así que vamos más o menos igual en nuestro aprendizaje: una cara.

Confío en que esta vez sí llegaré hasta el final en esta aventura de aprender a «resolver» el Rubik de 3×3. Ya voy sintiendo cómo algunas neuronas que tenía dormidas están despertando, así que el esfuerzo está sirviendo.

Les mantendré informados.

¡Feliz día Internacional de LEGO hoy y de los Rompecabezas mañana!

¡Hasta el siguiente miércoles!

PD: Quiero agradecer a esta página en la que me apoyo constantemente para redactar el blog: pixabay.

Esta es la entrada 405 de este blog. 405 es múltiplo de 9, número que me gusta más que todos los demás (ver por qué aquí), así que toca compartir algo especial, que hoy será una experiencia con una niña a la que le estuve enseñando a resolver ecuaciones lineales desde cero.

Empezamos con alto tipo x – 2 = 0 a lo que me respondió con un mero procedimiento mental: 2

Le dije que me parecía muy bien que llegara a la respuesta sin procedimiento, porque le podía servir para comprobar la respuesta con procedimiento (además le enseñé a comprobar por sustitución). Y luego le mostré el procedimiento de sumar 2 a ambos lados del igual para «despejar» la x.

Hicimos un par más con una sola x con coeficiente 1 y todas las resolvía sin procedimiento, por más que yo intentaba que lo usara de inicio porque era lo que yo estaba tratando de que aprendiera, un procedimiento que le sirviera aún en ejercicios más complejos.

Luego hicimos ejercicios tipo 4x = 8 para lo que me respondió inmediatamente: 2.

Otra tanda de ejercicios que resolvía mentalmente.

Entonces decidí ponerle un freno:

3x + 5 = 17

Su mente que podía hacer fácilmente una única operación, ya no supo en qué orden hacer operaciones para «adivinar» esta respuesta.

Sonreí y le dije: «por eso te estoy pidiendo que sigas el procedimiento, porque si tu mente se acostumbra a buscar las respuestas sin seguirlo, te puedes trabar a medio examen».

Nota importante: Nunca ha sido mi estilo enseñar un procedimiento único o a usar recetas estrictas al resolver, pero sí es mi estilo transmitir estrategias que ayuden bajo las circunstancias particulares de cada quien. En este caso se trata de una niña con un rezago académico importante, así que si bien busco fomentarle en momentos la libertad creativa para resolver planteamientos, también necesito darle estrategias para enfrentarse a exámenes para los que sus conocimientos y habilidades previas pueden no ser suficientes si no las sigue.

Como siempre, cada caso es distinto, lo que quiero compartir aquí es que, si un alumno se niega a aprender un procedimiento porque no le ve la utilidad porque puede resolver el ejercicio sin él, podemos plantearle un ejercicio que no se resuelva fácilmente si no se sigue dicho procedimiento, para que logre ver la relevancia y le haga sentido aprenderlo.

Ya después decidirá cuándo usarlo o no.

¡Hasta el próximo miércoles!

PD: Quiero agradecer a esta página en la que me apoyo constantemente para redactar el blog: pixabay.