Esta es la entrada 333 de este blog. 333 es un número genial: es múltiplo de 9, mi número favorito (ver por qué aquí) y además es capicúa (ver más sobre capicúas aquí), esto es, se lee igual de izquierda a derecha y de derecha a izquerda.

Las entradas múltiplo de 9 me gusta dedicarlas a algo especial. En este caso, tengo varias semanas con la idea de hablar sobre esta frase que tanto enorgullece a algunos que la dicen, generalmente refiriéndose a que no es relevante que les haya ido mal en matemáticas en la escuela y no hayan aprendido gran cosa de la materia, cuyos conceptos no sirven para el día a día:

Un día más sin usar el Trinomio Cuadrado Perfecto

Si me preguntan, yo también he vivido muchísimos días sin usar el TCP. Prácticamente solo en contextos escolares lo he usado, como la mayoría de la gente. Entonces estoy de acuerdo en que deje de enseñarse.

Es broma.

A continuación mi breve reflexión al respecto:

Enseñar a identificar un TCP y cómo factorizarlo es una excelente manera de practicar el concepto de reversibilidad en matemáticas (ver más aquí), que permea a muchos de los temas de esta materia y de otras.

Identificar las características de una expresión algebraica como las de un TCP y saber qué hacer con eso y cómo hacer los cálculos para su correcta su factorización ayuda a desarrollar los dos pilares de una buena relación con las matemáticas (pensamiento lógico matemático y sentido numérico, ver más aquí).

En sí dentro de la trayectoria académica el identificar qué sí y qué no es un TCP puede ayudar a que evitemos este error que es tremendamente común:

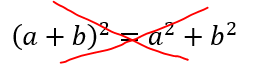
Pues como sabemos que el TCP se factoriza así:

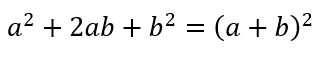
Por reversibilidad, la correcta expansión de un binomio al cuadrado es:

Y esto nos ayuda a trabajar el sentido de estructura (ver más aquí)

Por otro lado, buscando una imagen interesante para que encabezara la entrada, me di cuenta de que el nombre puede llevar a unas reflexiones que confundan la mente:

«Trinomio» (suena a tres-algo… quizá relacionado con un triángulo… sigamos leyendo a ver si entendemos)

«Cuadrado» (pues sí ha de ser un triángulo lo anterior, porque esto de cuadrado también es una figura geométrica… pero los triángulos no son cuadrados y esto es álgebra, no geometría… ¡qué confusión!)

«Perfecto» (las matemáticas siempre tan perfectas, por eso me cuestan tanto… ¡qué estrés!)

Por eso escogí esa imagen de portada, con triángulos y cuadrados y una armonía cromática linda, que no perfecta.

Con reflexiones como esas se entiende el rechazo a las matemáticas y la alegría por vivir un día más sin usar el TCP. Sin embargo, la realidad del significado del nombre es otra:

Trinomio viene de que es una expresión algebraica de tres términos

Cuadrado viene de que su primer y tercer miembros son cuadrados, es decir, provienen de una expresión que fue elevada al cuadrado.

Perfecto parece que viene de que los términos cuadrados son cuadrados perfectos (que tienen una raíz cuadrada exacta), pero también puede entenderse que viene de que el segundo término es el «perfecto» para que pueda ser factorizado como un binomio al cuadrado. Porque no todos los trinomios cuyo primer y tercer miembro son cuadrados se factorizan como un binomio al cuadrado. Por ejemplo:

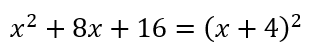
La expresión del lado izquierdo sí es un TCP, porque se factoriza como un binomio al cuadrado, que es la expresión del lado derecho.

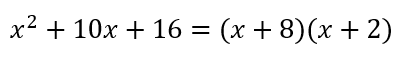
La expresión del lado izquierdo, aunque su primer y tercer términos son cuadrados, el término de en medio no nos permite factorizarla como un binomio al cuadrado, sino como binomios con término común.

Mucho, pero mucho en matemáticas es preparación, ejercitación mental para algo más, como las habilidades matemáticas que mencioné antes (reversibilidad, pensamiento lógico matemático, sentido numérico, sentido de estructura, etc.), necesarias dentro y fuera de la materia. Si al final decidimos dedicarnos a matemáticas puras o aplicadas, o a la docencia de la materia, entonces muy probablemente sí estaremos usando el TCP en nuestro día a día.

Si no, las conexiones mentales que nos proporciona el ejercitarnos analizando expresiones algebraicas para saber si son trinomios cuadrados perfectos, y después factorizarlos y hacer algo más con ello, sí que nos servirán para mejorar nuestra capacidad de observación, análisis y toma de decisiones que… ¿Quién no necesita su capacidad de observación, análisis y toma de decisiones en el día a día?

Gracias por haber leído hasta aquí. Para bien o para mal, hoy fue un maravilloso día en el que sí usé el Trinomio Cuadrado Perfecto.

Y ustedes también.

¡Hasta el siguiente miércoles!

Rebeca

PD1: Quiero agradecer a esta página en la que me apoyo constantemente para redactar el blog: pixabay