Esta es la entrada 340 de este blog. Agradezco a Malena Martín, de Aprendiendo Matemáticas, el haber encontrado esta página tan interesante:
WHICH ONE DOESN’T BELONG?
Que en español significa: ¿Cuál no pertenece?
Se trata de armar grupos de 4 imágenes u objetos físicos, dibujados, calculados… de manera que cada uno de ellos «no pertenezca» al grupo porque no comparte una de las características que los demás sí comparten.
Me parece un excelente ejercicio para desarrollar el pensamiento lógico matemático y el sentido numérico (si se incluyen números) tanto al generar el reto como al resolverlo (ver más sobre los dos pilares de una buena relación con las matemáticas aquí)
A continuación les propongo una idea que incluye el sentido numérico y una más centrada en el pensamiento lógico matemático. Pueden ver las soluciones un poco más abajo, ya que lo hayan intentado por su cuenta:
.
.
.
¿Ya lo intentaron? Van las soluciones.
Solución al primer reto:
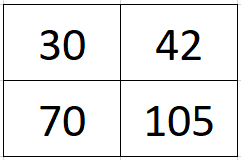
El 30 no pertenece por ser el único que no es múltiplo de 7
El 42 no pertenece por ser el único que no es múltiplo de 5
El 70 no pertenece por ser el único que no es múltiplo de 3
El 105 no pertenece por ser el único que no es múltiplo de 2
Como podrán deducir, lo que hice para ensamblar el reto fue tomar los primeros 4 números primos e ir multiplicando de 3 en 3.
Solución al segundo reto:
La carta de arriba a la izquierda no pertenece porque es la única con textura
La carta de arriba a la derecha no pertenece porque es la única con forma de zigzag
La carta de abajo a la izquierda no pertenece porque es la única morada
La carta de abajo a la derecha no pertenece porque es la única con dos imágenes
Este reto lo ensamblé con las cartas del T3rcia, un material lógicamente estructurado que, al tener 4 características que varían de 3 formas cada una, se presta muy bien para ensamblar este tipo de retos (ver más sobre los usos del T3rcia aquí). También podría hacerse con otros materiales lógicamente estructurados que tengan al menos 4 características, aunque solo varíen de 2 maneras, como con los bloques lógicos de Dienes (ver más sobre materiales lógicamente estructurados aquí):
La pieza de arriba a la izquierda no pertenece porque es la única gruesa
La pieza de arriba a la derecha no pertenece porque es la única circular
La pieza de abajo a la izquierda no pertenece porque es la única azul
La pieza de abajo a la derecha no pertenece porque es la única pequeña
Nota: armar los retos es un poco menos sencillo de lo que parece, se necesita un poco de práctica y encontrar el procedimiento que nos funcione mejor. Para armar el reto de los bloques lógicos me basé en dos características del que hice con el T3rcia (color y figura) y extrapolé las otras dos (textura por grosor y cantidad por tamaño). En ambos casos se pueden modificar las posiciones de las características distintas y los valores que toman, para hacer nuevos retos.
En todos los casos, se estará ejercitando la mente, que es para lo que estamos aquí.
¡Hasta el siguiente miércoles!
Rebeca