Al diseñar figuras geométricas, para que los alumnos practiquen el calcular áreas y perímetros, nos encontramos con una dificultad: las combinaciones numéricas (altura, base y lados) deben elegirse con cuidado para que la figura pueda construirse con ellas realmente. No todas las combinaciones funcionan.
Para facilitar el encontrar aquellas combinaciones de medidas enteras de lados y alturas de triángulos, que sí funcionan, podemos basarnos en las ternas pitagóricas, que son combinaciones de tres números enteros que cumplen con el Teorema de Pitágoras y que son fáciles de determinar si se conoce el procedimiento para generarlas.Leer más »
Al cerrar la entrada pasada sobre las características del sistema numérico decimal, que pueden ver 
Si ésta es la décima entrada de este blog, viene bien dedicarla al Sistema Numérico Decimal, con el que escribimos los números que usamos más comúnmente en matemáticas.
La razón de que nuestro sistema numérico tenga como base al número diez está, literalmente, en nuestras manos: tenemos 10 dedos, por lo que lo más natural y lógico es que contemos hasta diez y luego necesitemos algo más para seguir contando. Si tuviéramos 8 u 12 dedos, esos números serían la base. El sistema numérico decimal es, además, posicional, lo cual significa que cada dígito tiene un valor absoluto (por su forma) y un valor relativo (por su posición dentro del número).
La entrada pasada, que pueden ver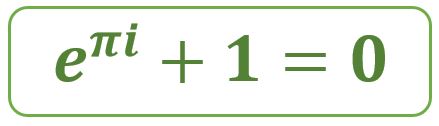 
Publico esta entrada un 14 de marzo, conocido en el mundo de las matemáticas como el día de pi (π), por escribirse la fecha en algunos países como 3.14. Esta coincidencia me llevó a elegir escribir sobre pi y otros números especiales.
Un desafío más emocionante es armar objetos con piezas intercambiables. Una misma pieza puede tener distintas funciones según su posición. La relación entre dos piezas puede ser diferente según la forma en que se unan, esto es, según la estructura del objeto.
Las expresiones matemáticas, en especial las algebraicas, también tienen una estructura y están formadas por piezas, o elementos, cuya función es variable y depende de a qué otros elementos están unidos y de qué forma.
Esta es la tercera de una serie de tres entregas sobre fracciones. Pueden leer la primera, sobre por qué son complejas de entender, 
La entrada anterior, que pueden leer 
Para las causas relacionadas con la forma como enseña el profesor, lo que se necesita es mejorar esa forma de enseñar. Ya escribí sobre evitar “arriba / abajo”. La próxima entrega escribiré sobre evitar los algoritmos que funcionan sólo bajo ciertas circunstancias. Antes es conveniente revisar otras bases necesarias para ello. Empecemos por algunos conceptos. 
IMPULSO MATEMÁTICO 