Quiero dedicar esta entrada a un tema que considero que a muchos de ustedes les gustará entender mejor: las fracciones.

¿Por qué se necesitan las fracciones?

Podría creerse que fueron inventadas para conseguir alejar a la gente de las matemáticas, dado que eso ocurre con ellas frecuentemente, pero no es así.

Analicemos, sin profundizar demasiado, porque no somos matemáticos, las operaciones básicas y los distintos tipos de números que resultan de ellas, para entender la necesidad de la existencia de las fracciones:

.
Primero están los números naturales, aquellos que usamos para contar: 1, 2, 3…

.
Al sumar un número natural a otro número natural, el resultado siempre es un número natural.

.
Eso cambia cuando hacemos una resta: al restar un número natural menos otro número natural, el resultado puede ser otro número natural, cero o un número negativo. Por lo tanto, los resultados de las restas de números naturales serán números enteros, que incluyen los naturales que ya habíamos mencionado, a los que agregamos el cero y los negativos de los naturales { … , -2, -1, 0, 1, 2, … } Los números enteros cubren la necesidad de abarcar todos los resultados de las restas de números naturales, incluso de números enteros.

Los números enteros son relativamente sencillos de entender, mediante la recta numérica.

.
Luego están las multiplicaciones, en las que, al multiplicar dos números enteros, siempre obtendremos un número entero. No hay necesidad de un nuevo tipo de números. Las multiplicaciones con números enteros también son relativamente sencillas de comprender, entendiendo las leyes de los signos.

.
Finalmente tenemos las divisiones. Cuando dividimos un número entero entre otro número entero, puede ser que el resultado sea otro número entero, pero puede ser que no. Debido a eso existen los números racionales (fracciones, quebrados), los cuales cubren la necesidad de abarcar todos los resultados de las divisiones de números enteros e incluso de números racionales. También están incluidos los resultados enteros, que pueden considerarse fracciones con denominador unitario implícito (no escrito), esto es, 5 se puede escribir como 5/1.

Además de dar cabida a los resultados de las divisiones, las fracciones se requieren para otros propósitos, como veremos en el siguiente apartado.

¿Qué son los números racionales (fracciones)?

Los números racionales se representan en la forma a/b (mucho cuidado, b debe ser diferente de cero para que el número esté definido). Tienen distintas interpretaciones matemáticas, de acuerdo al contexto en el que los encontremos:

Los números racionales son un cociente indicado: muestran que se pretende realizar un cociente (división), pero que se deja indicado, esto es, no se realiza, porque el resultado de dicho cociente no es entero. Si se va a dividir 2 entre 3, la respuesta más exacta es: 2/3.

Entender a las fracciones de esta forma es básico para entender posteriormente el álgebra, en la que frecuentemente se expresan operaciones que no pueden realizarse y, por tanto, quedan indicadas.

Son una razón: “2 de cada 3 personas compran manzanas” significa que 2/3 de las personas compran manzanas. Ver una fracción como una razón o como una comparación de conjuntos de objetos es la interpretación más compleja y delicada de todas, por sus implicaciones al hacer operaciones.

Representan cantidades que se pueden ubicar en la recta numérica, comparar, realizar operaciones con ellas, respetando sus características especiales. Como cantidades, pueden representar medidas: 2/3 de taza de arroz, por ejemplo.

Finalmente tenemos la interpretación más conocida, parte-todo, en la que 2/3 significa que se partió una unidad completa en tres partes iguales y se tomaron 2 de ellas. En la imagen que encabeza esta entrada, quien toma una rebanada de pastel toma 1/10 del mismo, porque se partió en 10 rebanadas iguales y se tomó una.

¿Por qué resultan complejas de comprender?

Imaginemos a un alumno que no conocía las fracciones y estaba acostumbrado a que los números estuvieran todos en un mismo nivel y a que, para cualquier operación que le presentaran, sabía cuándo había terminado el procedimiento del cálculo y obtenía un único resultado.

Cuando se encuentra con las fracciones, resulta que todo eso quedó atrás y las dudas remplazan a la certeza. Ahora algunas operaciones pueden quedar indicadas, los resultados no son únicos, ya que distintas fracciones representan la misma cantidad, como 2/3 y 4/6, y es menos claro reconocer cuándo terminó un procedimiento, como cuando está simplificando una fracción y no está seguro de haber llegado a la expresión más simple, por no conocer las condiciones de divisibilidad.

Además, los procedimientos para operar las fracciones son muy distintos a los procedimientos para operar los enteros. Ya no es posible usar los dedos para hacer los cálculos y usar una recta numérica para ello tampoco es sencillo. Incluso dentro de las mismas fracciones, para sumar y restar se necesita tener un denominador común, pero para multiplicar y dividir no.

«Los números racionales son el primer conjunto de experiencias numéricas que no están basadas en los algoritmos de recuento como los números naturales»

Juan D. Godino, Didáctica de las Matemáticas para Maestros

Todo esto, aunado a las distintas interpretaciones matemáticas de un número racional mencionados en el apartado anterior, es lo que vuelve compleja la comprensión de las fracciones. Transitar de una interpretación a otra puede ser complicado. Por ejemplo, la interpretación parte-todo, que suele ser la inicial e introducirse mediante dibujos de áreas unitarias partidas y sombreadas, es muy sencilla de comprender y usar… hasta que se requiere representar una fracción mayor a la unidad, comparar fracciones o hacer operaciones con ellas y, por tanto, es necesario dejar la seguridad de esa interpretación para trasladarse a otras.

Si el alumno cuenta con un profesor que entiende las fracciones, sus características y la lógica de las operaciones con ellas y busca que el alumno también las entienda, es probable que la relación del estudiante con las matemáticas siga siendo agradable. Cuando el profesor no tiene la comprensión completa y/o se limita a transmitir algoritmos sin fundamentarlos, es cuando las matemáticas comienzan a ser un dolor de cabeza para los alumnos.

Esperen, creo que debo explicar un poco mejor las situaciones que vuelven complejas las fracciones, que no son propias de las características de las fracciones, sino del manejo que le dan los profesores:

Una es el hablar de “arriba y abajo” en vez de hablar de “numerador y denominador”. “Arriba y abajo” son posiciones físicas de los números y expresarse así de ellos no ayuda a la comprensión de la relación que hay entre esos números que forman la fracción. Comprender el significado de “numerador y denominador” le da sentido y facilita el trabajo con las fracciones.

(Nota al margen: acepto que toda mi vida escolar dije: “arriba” y “abajo” y ha sido muy complicado autocorregirme ahora como docente. Confío en que cada vez sean más profesores los que usen adecuadamente el lenguaje matemático, apoyando con esto a la comprensión conceptual de sus alumnos)

La otra es el uso indiscriminado de algoritmos sin explicar su fundamento ni señalar que funcionan sólo en ciertas circunstancias, pero no en todas. Dos ejemplos son el «método mariposa», que puede usarse para sumar o restar dos fracciones, pero que no puede usarse para sumar y/o restar más de dos fracciones y el «método de la multiplicación cruzada», con el que se dividen dos fracciones, pero no pueden dividirse más de dos fracciones.

¿Numerador/denominador o arriba/abajo?

Usaré la interpretación parte-todo de las fracciones porque considero que es con la que mejor se comprenden los nombres:

El denominador, como su nombre lo indica, denomina, esto es, le da nombre a la fracción, indicando en cuántas partes se dividió la unidad. Y sí, es el número que se escribe abajo de la línea de la fracción, pero debemos evitar llamarle así.

El numerador, como su nombre lo indica, numera, esto es, cuenta cuántas partes se tomaron. Sí, es el número que se escribe arriba de la línea de la fracción, pero también debemos evitar llamarle así.

El entender que el denominador le da nombre a la fracción puede ayudar a la comprensión de que sólo se pueden sumar fracciones con denominadores idénticos. Veamos este ejemplo (¡Cuidado! sólo aplica para sumas y restas de fracciones, las multiplicaciones y divisiones funcionan distinto):
Así como entendemos que se pueden sumar dos manzanas más tres manzanas para obtener cinco manzanas, pero si sumamos dos manzanas más tres peras NO obtenemos cinco manzanaperas, así debemos entender que al sumar dos séptimos más tres séptimos obtenemos cinco séptimos, pero si sumamos dos séptimos más tres octavos NO obtenemos cinco quinceavos.

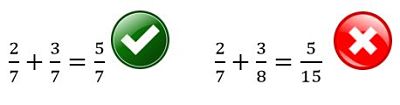
Creo que cuando la operación está escrita con palabras queda muy claro lo que es correcto hacer y lo que no. Cuando está escrita con números, podemos leer la operación en voz alta («convertir» los números en palabras) remarcando lo necesario para recordar lo que debemos cuidar: lo que se suma (o resta) son los numeradores de las fracciones. La condición para sumarlos (o restarlos) es que los denominadores de las fracciones a sumar (o restar) sean iguales.

¿Cómo influyen numerador y denominador en el tamaño de la fracción?

Escuché una historia sobre el dueño de un restaurante que quiso hacerle competencia a otro que vendía hamburguesas de “un cuarto de libra” de carne. Lo intentó vendiendo hamburguesas de “un tercio de libra” de carne, al mismo precio que las de «un cuarto de libra» de su competidor. La estrategia fue un fracaso porque muchos de los clientes entendieron que estaban pagando la misma cantidad de dinero por menos carne. Su razonamiento era este: si 3 es un número más pequeño que 4, entonces 1/3 de libra debe ser menos que 1/4 de libra. No entendían que un restaurante partía una libra de carne en 4 y el otro en 3 y por lo tanto, el que la partía en 3 estaba incluyendo más carne en sus hamburguesas… por el mismo precio.

Otra anécdota relacionada con el tema es la del empleado de la pizzería que le pregunta al cliente que en cuántas rebanadas le parte la pizza, en 8 o en 12 y recibe por respuesta: “En 8, no creo poder comerme 12”. Si se iba a comer todas las rebanadas, comer 8/8 de pizza o 12/12 de pizza es la misma cantidad de comida… siempre y cuando la pizza sea del mismo tamaño. Esta mezcla de geometría con fracciones debe tratarse con cuidado.

Con este par de anécdotas podemos ver cómo la incomprensión de las fracciones, su significado y su valor, puede llevarnos a tomar decisiones incorrectas. ¿Cómo entenderlas mejor?

Necesitamos recordar que el denominador, además de darle el nombre a la fracción, indica en cuántas partes se dividió la unidad. Una fracción con un denominador más grande indica que la unidad se dividió en más partes y, por tanto, cada parte es más pequeña. Al comparar dos fracciones con numeradores iguales, la mayor será la que tenga el denominador más chico, como en el caso de las hamburguesas.

Por otro lado, el numerador indica cuántas partes de la unidad se tomaron. Al comparar dos fracciones con denominadores iguales, la mayor será la que tenga el numerador más grande, porque se tomaron más partes y todas eran del mismo tamaño.

Para desvincular la magnitud de la fracción con la idea de partir un objeto y tomar una cierta cantidad de partes, y con ello ampliar la comprensión de los números racionales, podemos identificar la posición de las fracciones en una línea recta y así compararlas. Al igual que con los enteros, mientras más a la derecha del cero esté el número, mayor será, por lo que 3/5 < 4/5 y 3/5 < 3/4. De hecho, el proceso para ubicar las fracciones en la recta también implica «partir» la unidad y «tomar» cierta cantidad, sólo que en este caso la unidad es una línea, no un área. La comprensión del valor de las fracciones mayores a la unidad es más sencilla sobre una recta.

El comparar fracciones con distinto numerador y denominador lo abordaré en una siguiente entrada.

Para cerrar

Se dice que entender un problema es el primer paso para resolverlo, por eso estoy abordando el tema de las fracciones de esta forma. Confío en que después de leer esta entrada tengan una mejor comprensión del porqué el encuentro con las fracciones puede marcar en positivo o en negativo la relación de los estudiantes con las matemáticas. Es un tema complejo y extenso. Dedicaré otras entradas a las operaciones con fracciones. Consideré necesario sentar estas bases primero.

Quiero comentar que busco, al escribir, usar un lenguaje que evite tanto la informalidad del lenguaje coloquial, que hace que las matemáticas pierdan su significado real, como la formalidad de un matemático puro, que sería difícil de entender para los lectores a los que quiero que llegue mi mensaje. Confío en haber logrado explicar con claridad las distintas características de las fracciones y las implicaciones de esas características en la forma de trabajar con ellas.

Agradezco de antemano que me escriban sus comentarios y me compartan sus experiencias y sus dudas. Bajo el título de cada entrada se encuentra la opción «comentarios», donde pueden hacerlo.

Rebeca

PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.

PD2: Quiero agradecer a estas dos páginas en las que me apoyo constantemente para redactar el blog: https://pixabay.com/   http://webresizer.com/

Realicé algunas imágenes en Word y en Geogebra.

Photo by marcoverch on Foter.com / CC BY (Foto de las tazas medidoras)