 Ésta es la entrada 65 del blog. La dedicaremos a tratar un tema que, dependiendo de cómo se le aborde, puede asustar a muchos. Como podrán imaginar, buscaré abordarlo de manera que no asuste, antes bien, despierte la curiosidad. Les adelanto que esta entrada no contendrá el desarrollo de ningún tema de la materia propiamente, más bien nos concentraremos en entender qué es el cálculo (diferencial e integral), qué fue necesario que pasara para que fuese descubierto, cuáles son sus aplicaciones y cómo podemos preparar a nuestros hijos y alumnos, desde la primaria y la secundaria, para que su paso por los cursos de cálculo sean suaves y enriquecedores.
Ésta es la entrada 65 del blog. La dedicaremos a tratar un tema que, dependiendo de cómo se le aborde, puede asustar a muchos. Como podrán imaginar, buscaré abordarlo de manera que no asuste, antes bien, despierte la curiosidad. Les adelanto que esta entrada no contendrá el desarrollo de ningún tema de la materia propiamente, más bien nos concentraremos en entender qué es el cálculo (diferencial e integral), qué fue necesario que pasara para que fuese descubierto, cuáles son sus aplicaciones y cómo podemos preparar a nuestros hijos y alumnos, desde la primaria y la secundaria, para que su paso por los cursos de cálculo sean suaves y enriquecedores.
Considero que Cálculo Diferencial y Cálculo Integral son un par de materias que han disuadido a más de uno de estudiar la carrera que realmente quería. Espero de corazón que lo que comparto en este blog, en esta entrada, las anteriores y las posteriores, disminuya la ocurrencia de esa triste situación.
Comencemos por identificar:
¿Qué problema estaban buscando resolver los que descubrieron el cálculo?
Bueno, más que un problema, eran cuatro problemáticas distintas las que se estaban buscando resolver cuando el cálculo fue descubierto, resolviendo las cuatro al mismo tiempo:
¿Cómo medir el área bajo una curva?
 Las áreas bajo o dentro de figuras con lados rectos pueden seccionarse de forma tal que queden triángulos y rectángulos que permitan encontrar el área de la figura completa, basándonos sólo en conocimientos de la educación primaria, pero ¿qué pasa cuando alguno de los lados no es recto, sino curvo? Para ciertas figuras, como el círculo, se lograron encontrar fórmulas. Las demás necesitaron esperar al cálculo para conocer su área exacta.
Las áreas bajo o dentro de figuras con lados rectos pueden seccionarse de forma tal que queden triángulos y rectángulos que permitan encontrar el área de la figura completa, basándonos sólo en conocimientos de la educación primaria, pero ¿qué pasa cuando alguno de los lados no es recto, sino curvo? Para ciertas figuras, como el círculo, se lograron encontrar fórmulas. Las demás necesitaron esperar al cálculo para conocer su área exacta.
Quizá para saber cuál es el área bajo la curva del arco iris no sea necesario el cálculo, porque entiendo que tiene forma circular, pero es una curva bonita para ilustrar esta sección, ¿no creen?
(Paréntesis cultural: encontrar la cuadratura del círculo significa encontrar una figura cuadrada con la misma área que un círculo de un diámetro dado. Por lo tanto, encontrar el área bajo una curva sería cuadrar la curva).
¿Cómo calcular la velocidad a la que se mueve un objeto en un instante dado?
 La velocidad promedio se calcula como la distancia recorrida entre el tiempo usado para recorrerla, es algo que se aprende en la educación secundaria, pero ¿el objeto se movió a esa misma velocidad todo el tiempo que duró en movimiento? Normalmente no ocurre eso, entonces ¿a qué velocidad iba en cada instante distinto?
La velocidad promedio se calcula como la distancia recorrida entre el tiempo usado para recorrerla, es algo que se aprende en la educación secundaria, pero ¿el objeto se movió a esa misma velocidad todo el tiempo que duró en movimiento? Normalmente no ocurre eso, entonces ¿a qué velocidad iba en cada instante distinto?
¿Cómo determinar la pendiente de una curva?
 Las pendientes, o inclinaciones, son sencillas de calcular cuando se tiene una forma recta, como en varias de las rampas para patineta de la imagen. Es algo que también se aprende en la educación secundaria: sólo se divide el incremento en vertical entre el incremento en horizontal entre cualquier par de puntos de la recta y listo (ver más sobre líneas rectas y sus pendientes aquí), pero ¿qué pasa cuando la línea no es recta, sino curva? ¡La pendiente es diferente en cada punto! ¿Cómo determinarla?
Las pendientes, o inclinaciones, son sencillas de calcular cuando se tiene una forma recta, como en varias de las rampas para patineta de la imagen. Es algo que también se aprende en la educación secundaria: sólo se divide el incremento en vertical entre el incremento en horizontal entre cualquier par de puntos de la recta y listo (ver más sobre líneas rectas y sus pendientes aquí), pero ¿qué pasa cuando la línea no es recta, sino curva? ¡La pendiente es diferente en cada punto! ¿Cómo determinarla?
¿Cómo encontrar el valor de la variable independiente en el que la variable dependiente tiene un valor máximo o mínimo local?
 Si tenemos una función que modela un comportamiento: ingresos, costos, utilidades, todas en función de la cantidad vendida, altura al lanzar un objeto, en función del tiempo transcurrido, la altura inicial y velocidad inicial, así como la gravedad, etcétera, ¿cómo saber en qué punto exacto ese comportamiento tiene un valor máximo o mínimo dentro de un intervalo de valores o a lo largo de toda la función? Con ello podríamos saber la altura máxima que alcanzará el objeto, así como la cantidad que debemos vender para maximizar nuestras utilidades, o las fechas en las que una acción tuvo valores más altos que el día anterior y el posterior.
Si tenemos una función que modela un comportamiento: ingresos, costos, utilidades, todas en función de la cantidad vendida, altura al lanzar un objeto, en función del tiempo transcurrido, la altura inicial y velocidad inicial, así como la gravedad, etcétera, ¿cómo saber en qué punto exacto ese comportamiento tiene un valor máximo o mínimo dentro de un intervalo de valores o a lo largo de toda la función? Con ello podríamos saber la altura máxima que alcanzará el objeto, así como la cantidad que debemos vender para maximizar nuestras utilidades, o las fechas en las que una acción tuvo valores más altos que el día anterior y el posterior.
Todas las problemáticas anteriores tienen más o menos importancia según el contexto.
 Algunas veces obtener esos resultados de forma aproximada es suficiente. Sin embargo, las aproximaciones no sirven para hacer cosas como mandar un cohete a la Luna o poner un satélite en órbita para que proporcione servicio de Internet (creo que ya capté la atención de varios lectores: Internet se ha vuelto una necesidad básica de un tiempo para acá).
Algunas veces obtener esos resultados de forma aproximada es suficiente. Sin embargo, las aproximaciones no sirven para hacer cosas como mandar un cohete a la Luna o poner un satélite en órbita para que proporcione servicio de Internet (creo que ya capté la atención de varios lectores: Internet se ha vuelto una necesidad básica de un tiempo para acá).
Sigamos explorando el tema.
¿A nadie se le había ocurrido cómo resolver esos problemas antes del siglo XVII?
La verdad es que sí hubo muchos intentos, con más o menos éxito:
 El área de superficies con orillas curvas se logró determinar con bastante exactitud en la antigua Grecia hace unos 2500 años, por un método llamado exhaustivo (o por agotamiento), que no significaba propiamente que los matemáticos quedaban exhaustos o agotados después de hacer los cálculos. Más bien significaba que hacían triangulitos o rectangulitos cada vez más pequeños, hasta cubrir el área en cuestión lo más exhaustivamente posible. Sumaban todas esas áreas y con ello aproximaban el área total.
El área de superficies con orillas curvas se logró determinar con bastante exactitud en la antigua Grecia hace unos 2500 años, por un método llamado exhaustivo (o por agotamiento), que no significaba propiamente que los matemáticos quedaban exhaustos o agotados después de hacer los cálculos. Más bien significaba que hacían triangulitos o rectangulitos cada vez más pequeños, hasta cubrir el área en cuestión lo más exhaustivamente posible. Sumaban todas esas áreas y con ello aproximaban el área total.
Suficientemente bueno para las necesidades de la época.
Pero… para los matemáticos, “suficientemente bueno” puede no ser realmente suficiente, así que siguieron buscando hasta dar con un método que pudieran sí considerar exacto, que fue encontrado en el Cálculo Integral.
Galileo Galilei (1564-1642), años antes del descubrimiento del cálculo había encontrado la forma de expresar lo que equivaldría a la función integrada de la velocidad instantánea.
Con respecto a la pendiente de una curva, Isaac Barrow (1630 – 1667) que, por cierto, fue profesor de Isaac Newton, encontró un método que también puede considerarse previo, pero que estaba limitado a ciertos casos.
Por otro lado, Pierre de Fermat (1607-1665) desarrolló un método que le permitía encontrar los máximos y mínimos de una función, que puede considerarse una base para el que se usó después ya con cálculo diferencial. La desventaja del método de Fermat es que, al igual que lo hecho por Barrow, estaba limitado a ciertos casos.
Hubo más aportaciones, pero dejaremos hasta aquí la lista, con la cual buscaba explicar por qué Isaac Newton dijo esta frase:
«Si he visto más lejos es porque estoy sentado sobre los hombros de gigantes»
reconociendo que sus descubrimientos estaban basados en los de sus predecesores.
¿Quién(es) se considera(n) padre(s) del Cálculo?
Es una historia razonablemente conocida: el Cálculo tiene dos padres:
 Isaac Newton (1643-1727) Más popular por la Ley de la Gravitación Universal, sus tres leyes de la dinámica y, por supuesto, por la manzana que se dice que le cayó en la cabeza y lo inspiró para entender la ley de la gravedad. El prolífico Newton también trabajó en diversos temas de matemáticas, descubriendo los principios del Cálculo Diferencial mientras buscaba determinar velocidades instantáneas.
Isaac Newton (1643-1727) Más popular por la Ley de la Gravitación Universal, sus tres leyes de la dinámica y, por supuesto, por la manzana que se dice que le cayó en la cabeza y lo inspiró para entender la ley de la gravedad. El prolífico Newton también trabajó en diversos temas de matemáticas, descubriendo los principios del Cálculo Diferencial mientras buscaba determinar velocidades instantáneas.
Gottfrey Leibniz (1646-1716) Quizá menos popular que Newton, también aportó muchos avances en distintas ciencias. Descubrió el Cálculo Integral mientras buscaba cómo determinar, de forma exacta, áreas bajo curvas.
 Ambos llegaron a un punto en el que se dieron cuenta que el cálculo diferencial y el cálculo integral son procesos inversos. Juntas, ambas disciplinas se llamaron por un tiempo Cálculo Infinitesimal, veremos más adelante por qué.
Ambos llegaron a un punto en el que se dieron cuenta que el cálculo diferencial y el cálculo integral son procesos inversos. Juntas, ambas disciplinas se llamaron por un tiempo Cálculo Infinitesimal, veremos más adelante por qué.
 Ah, pero antes les comento que, como Newton tardó en publicar sus descubrimientos alrededor de esta materia y Leibniz fue más rápido en mostrar sus hallazgos al público, se desató una disputa intensa entre los seguidores de ambos sobre la paternidad de ese conocimiento. Los expertos actuales consideran que ninguno le copió al otro. Ambos desarrollaron, a partir de todos los conocimientos generados por la humanidad hasta entonces, sus propios métodos, que en los documentos de cada uno podrán verse muy distintos, dados sus diferentes enfoques, pero, en esencia son lo mismo y son la base de lo que aprendemos actualmente en la escuela.
Ah, pero antes les comento que, como Newton tardó en publicar sus descubrimientos alrededor de esta materia y Leibniz fue más rápido en mostrar sus hallazgos al público, se desató una disputa intensa entre los seguidores de ambos sobre la paternidad de ese conocimiento. Los expertos actuales consideran que ninguno le copió al otro. Ambos desarrollaron, a partir de todos los conocimientos generados por la humanidad hasta entonces, sus propios métodos, que en los documentos de cada uno podrán verse muy distintos, dados sus diferentes enfoques, pero, en esencia son lo mismo y son la base de lo que aprendemos actualmente en la escuela.
(La imagen la encontré en pixabay, prueba de lo difundido que está el conflicto, que describí muy brevemente aquí por cuestiones de espacio)
¿Por qué el Cálculo se pudo descubrir hasta el siglo XVII?
Como vimos en el apartado anterior, se necesitaron muchos avances matemáticos, uno tras otro, para poder sentar las bases para descubrir el cálculo. Haré una lista de algunas de las principales. Si conocen alguna más, agradeceré que la compartan en los comentarios:
Aritmética: para calcular valores y como apoyo para las manipulaciones algebraicas.
Álgebra: para escribir las funciones y manipularlas antes y después de derivar o integrar, que son los procesos propios del cálculo.
Geometría: para plantear funciones relacionadas con longitudes, áreas y volúmenes.
Trigonometría: para plantear funciones relacionadas con ángulos.
Geometría analítica: permitió llevar la geometría al plano cartesiano, para trabajar con ella algebraicamente y, con ello, ser susceptible de ser derivada o integrada.
A propósito de lo anterior, en el título de la entrada incluí la pregunta:
¿Cómo puede un profesor de primaria o secundaria apoyar a sus alumnos para estar preparados para estudiarlo?
 La respuesta es: comprendiendo cómo mucho de lo que enseña es básico para que el alumno pueda cursar con fluidez las materias de Cálculo. Porque cuando un alumno está resolviendo ejercicios en estas materias, quizá un 50% de lo que hace sea algo que acaba de aprender a hacer (derivar e integrar). El otro 50%, incluso más, lo aprendió en la primaria, secundaria y los primeros años del bachillerato.
La respuesta es: comprendiendo cómo mucho de lo que enseña es básico para que el alumno pueda cursar con fluidez las materias de Cálculo. Porque cuando un alumno está resolviendo ejercicios en estas materias, quizá un 50% de lo que hace sea algo que acaba de aprender a hacer (derivar e integrar). El otro 50%, incluso más, lo aprendió en la primaria, secundaria y los primeros años del bachillerato.
La materia que más he impartido en mi práctica docente es Cálculo Diferencial. Me resulta muy triste observar, en las producciones de los alumnos, cómo muchos logran hacer lo que acaban de aprender conmigo (derivar e interpretar los resultados), pero los procesos anteriores o posteriores a la derivación los hacen mal y, con ello, el resultado final está mal. Por eso es tan importante para un profesor de cálculo el apoyo de todos los profesores de las materias previas de matemáticas. Si ellos logran un buen aprendizaje de los temas que les corresponden en sus alumnos, las materias de cálculo dejarán de ser un dolor de cabeza.
El sistema numérico decimal, el cero, el infinito y los infinitésimos.
Además de todo lo mencionado en el apartado anterior, para que se descubriera el cálculo fue necesario, primero, que se adoptara el sistema numérico decimal, con su característico cero (ver más sobre el cero aquí) y su facilidad para escribir todo tipo de cantidades (ver más sobre el Sistema Numérico Decimal aquí). Imagínense a Newton intentando hacer derivadas con números romanos (ver más sobre números romanos aquí), ¡una locura! En cambio, con el práctico sistema de numeración decimal, llevado de la India a Arabia e introducido en Europa por Fibonacci en el siglo XIII, el desarrollo de la matemática despegó como nunca antes.
El cero, el sistema numérico decimal y los intentos previos de resolver los problemas mencionados anteriormente no fueron suficientes. Para poder desarrollar conceptualmente el cálculo se necesitó comprender dos conceptos más:
 El infinito, que no es un número como tal, pero representa a aquella cantidad que es más grande que cualquier número. Hay infinitos de distinto orden (unos más grandes que otros) pero explicar eso lo dejaremos para una entrada posterior.
El infinito, que no es un número como tal, pero representa a aquella cantidad que es más grande que cualquier número. Hay infinitos de distinto orden (unos más grandes que otros) pero explicar eso lo dejaremos para una entrada posterior.
El infinitésimo, que tampoco es un número como tal, pero representa a aquella cantidad que es más chica que cualquier número, sin llegar a ser cero. Digamos que es un número infinitamente pequeño.
En un principio, el cálculo se desarrolló con base en los infinitesimales, de ahí el nombre de cálculo infinitesimal. Posteriormente, con la introducción de los límites, los infinitesimales dejaron de usarse. De hecho, yo no aprendí cálculo con infinitesimales ni en el bachillerato ni en la universidad. Los conocí en la Maestría en Enseñanza de las Matemáticas, gracias a que tuve una maestra rusa y en Rusia es aún común su uso. Gracias por eso, Dra. Nesterova.
¿Por qué son importantes los infinitésimos y los infinitos en el cálculo?
Trataré de explicarlo de una manera sencilla.
Empecemos por el área bajo la curva:
Puedo calcularla si hago una serie de rectángulos que tengan una altura relacionada con la posición de la curva (puede ser el inicio, el centro o el final del rectángulo) y un ancho dado. Mientras más pequeño sea el ancho que escoja, más rectángulos usaré y más cercano al valor exacto será mi cálculo, pero siempre sobrará o faltará un poco. ¿Cómo hacer que sea exacto?
 Si logro que el ancho sea prácticamente cero, sin ser cero, es decir, que su ancho sea un infinitésimo, el número de rectángulos será prácticamente infinito y no faltará ni sobrará nada. Obtendré el área exacta.
Si logro que el ancho sea prácticamente cero, sin ser cero, es decir, que su ancho sea un infinitésimo, el número de rectángulos será prácticamente infinito y no faltará ni sobrará nada. Obtendré el área exacta.
Eso es una integral: una suma de infinitos rectángulos de ancho infinitesimal, conseguida mediante un método que no implica hacer un número infinito de operaciones, sino un pequeño proceso llamado “integración” de la función que modela la curva para la que estamos calculando el área.
En ocasiones me lo he imaginado como si usara espaguetis, cortados a diferentes alturas siguiendo la curva, para calcular el área bajo la misma.
Ahora la pendiente de la curva.
 Creo que la forma más fácil de entender este concepto es pensar en el lanzamiento de, por ejemplo, el martillo en las olimpiadas. Está girando y, en el momento que se le suelta, no sigue la curva que estaba siguiendo al estar sujeto, sino que se va en línea recta, tangencialmente a la curva. La «pendiente» de esa línea recta equivale a la «pendiente» de la curva en el punto en el que el martillo fue soltado. Extrapolando para cualquier curva, su pendiente en un punto dado es igual a la pendiente de la recta tangente a ella en ese punto (recordarán que en la primaria aprendieron que una recta tangente toca a una curva en un solo punto, sin cruzarla).
Creo que la forma más fácil de entender este concepto es pensar en el lanzamiento de, por ejemplo, el martillo en las olimpiadas. Está girando y, en el momento que se le suelta, no sigue la curva que estaba siguiendo al estar sujeto, sino que se va en línea recta, tangencialmente a la curva. La «pendiente» de esa línea recta equivale a la «pendiente» de la curva en el punto en el que el martillo fue soltado. Extrapolando para cualquier curva, su pendiente en un punto dado es igual a la pendiente de la recta tangente a ella en ese punto (recordarán que en la primaria aprendieron que una recta tangente toca a una curva en un solo punto, sin cruzarla).
Una vez entendido lo anterior, podemos comprender que tenemos un problema si queremos calcular la pendiente de una recta de la cual conocemos sólo un punto, ya que para usar la fórmula se necesitan dos. Aquí llegan al rescate los infinitesimales. ¿Y si calculamos la pendiente de una recta entre dos puntos, cuya distancia sea infinitesimal? Lograremos ambas cosas: calcular una pendiente teniendo dos puntos y que dichos puntos sean prácticamente un punto, por estar distanciados entre sí prácticamente cero. Al hacerlo de forma general, para cualquier punto de una función, estamos haciendo el proceso llamado «derivación».
Eso en la actualidad se estudia usando límites (ver más sobre límites aquí y aquí). Incluso algunos cursos se saltan esta explicación y pasan directamente a las reglas que generalizan el uso de los límites.
Sobre los otros dos problemas que buscaban solución: la velocidad instantánea se calcula de la misma forma que la pendiente de la recta tangente a una curva. De hecho, Newton usó cálculo en su estudio de los movimientos de los planetas alrededor del sol. Por su parte, los extremos relativos (máximos y mínimos) se localizan donde la pendiente de la recta tangente es igual a cero, o está indefinida.
Las generalizaciones de los procesos de derivación e integración y el descubrimiento que son procesos inversos fueron la verdadera aportación de Newton y Leibniz al cálculo. Por lo que son llamados los padres del mismo.
También fue importante lo siguiente:
Notaciones
Una vez descubiertos los procesos, se necesitaba un lenguaje matemático para indicarlos al escribir. Parece que Newton no fue muy metódico en eso, al grado que su nomenclatura es poco usada en la actualidad. A la función derivada le llamaba fluxión, a los cambios de coordenada de la curva les llamaba fluentes y a la integración le llamaba método de fluentes. A Leibniz, por otro lado, le importaban mucho los signos, los símbolos y la buena comunicación de las ideas, por lo que fue más cuidadoso al diseñar su nomenclatura. Lagrange y Euler aportaron sus propias notaciones, siendo la de Euler muy poco usada.

¿Qué hace diferente al cálculo de todo lo anterior que se había hecho en matemáticas?
 La geometría nos permite, entre otras cosas, saber cuánto mide algo. Es estática.
La geometría nos permite, entre otras cosas, saber cuánto mide algo. Es estática.
El álgebra nos permite, entre otras cosas, saber cómo está estructurado algo y como se relacionan dos o más variables. También es estática.
 El cálculo nos permite, entre otras cosas, saber cómo se mueve algo. Es dinámico.
El cálculo nos permite, entre otras cosas, saber cómo se mueve algo. Es dinámico.
El cálculo nos permite sacar conclusiones como éstas:
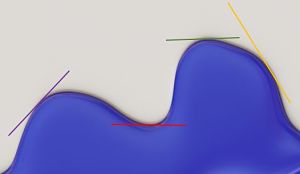 Si la pendiente de la tangente a la curva en un punto dado es positiva, los valores de la función van aumentando (crecen) conforme la variable independiente aumenta (línea morada).
Si la pendiente de la tangente a la curva en un punto dado es positiva, los valores de la función van aumentando (crecen) conforme la variable independiente aumenta (línea morada).
Si la pendiente de la tangente a la curva en un punto dado es negativa, los valores de la función van disminuyendo (decrecen) conforme la variable independiente aumenta (línea amarilla).
Si la pendiente de la tangente a la curva es cero, se puede tratar de un punto máximo (línea verde) o un mínimo (línea roja).
Si el área bajo la curva es positiva, la función está por encima del eje horizontal.
Si el área bajo la curva es negativa, la función está por debajo del eje horizontal.
Todo lo anterior tiene implicaciones muy interesantes, dependiendo del contexto. Ayuda a decidir cuánto producir para maximizar la utilidad, a determinar la velocidad de propagación de una epidemia, a calcular el volumen de un sólido generado por la revolución de una función sobre uno de los ejes, a minimizar el área lateral para un volumen dado, a maximizar el área con un perímetro fijo, a minimizar el perímetro con un área fija, calcular el diseño y la colocación de los satélites…
Para cerrar
Fue todo un reto escribir esta entrada. Confieso que, aunque tengo desde el 2003 enseñando Cálculo Diferencial y/o Integral la mayoría de los semestres, me concentraba, como el programa lo indicaba, en los ejercicios y las aplicaciones. Pero este semestre es el primero que enseño Cálculo a una generación francamente Centennial (ver más sobre los Centennials aquí) y limitar mi curso a ejercicios y aplicaciones ya no fue suficiente. Afortunadamente, a esta generación le interesa entender con mayor profundidad lo que están haciendo, así que fue necesaria esta labor de comprensión más completa de mi parte, para poder después acompañarlos de mejor manera.
Decidí compartir mis aprendizajes aquí para que los maestros de primaria y secundaria, para quienes están dirigidas regularmente las entradas, puedan conocer hacia dónde van sus alumnos y comprendan la importante labor que realizan al prepararlos para ello.
Como siempre, gracias por leer y compartir con quien pueda considerar útil esta información.
¡Hasta el siguiente miércoles!
Rebeca
PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.
PD2: Quiero agradecer a estas páginas en las que me apoyo constantemente para redactar el blog: pixabay y webresizer
Los nombres, fechas y datos históricos los tomé de wikipedia



I loved it! Thank you for making me understand several topics in just one article! Thank you Rebeca.
Me gustaMe gusta
Info muy amigable para los legos en mates. Gracias.
Me gustaLe gusta a 1 persona
Gracias, Jose, es la idea.
Saludos
Me gustaMe gusta
4x^3 calcular la diferencial y la integral
Me gustaMe gusta
Hola, Raúl
Para y=4x^3
La diferencial es dy=12x^2 dx
La integral es x^4 + C
Saludos
Me gustaMe gusta
[…] fue tremendamente útil. Ocurrió poco tiempo antes que el descubrimiento del cálculo (ver más aquí) y facilitó de forma importante los cálculos a ingenieros, astrónomos y demás personas que […]
Me gustaMe gusta