Ésta es la entrada número 51, la última antes de que el blog llegue a 52 semanas publicándose y nos preparemos para soplar la vela de su primer cumpleaños. Al pensar en algo a lo que nos estamos acercando, me llegó a la mente el concepto de límite que se usa en Cálculo Diferencial e Integral y decidí escribir sobre eso en esta entrada y la siguiente.
Considero que con el concepto de límite pasa algo similar a lo que ocurre con los conceptos de sucesión, serie y patrón (ver más aquí y aquí). Son conceptos que permiten interpretaciones que pueden resultar muy diferentes. Es decir, en el lenguaje coloquial significan algo que nos dificulta entender lo que significa en el lenguaje matemático.
 Por ello debemos tener diversos cuidados al entender, aprender y enseñar los conceptos y procedimientos relacionados con límites en matemáticas. En la entrada de hoy revisaremos las dificultades a las que solemos enfrentarnos para poder entender este concepto, así como las bases para sí lograr entenderlo adecuadamente. En la siguiente complementaremos con los distintos casos que necesitamos identificar al momento de determinar los límites y la forma de trabajar en cada uno.
Por ello debemos tener diversos cuidados al entender, aprender y enseñar los conceptos y procedimientos relacionados con límites en matemáticas. En la entrada de hoy revisaremos las dificultades a las que solemos enfrentarnos para poder entender este concepto, así como las bases para sí lograr entenderlo adecuadamente. En la siguiente complementaremos con los distintos casos que necesitamos identificar al momento de determinar los límites y la forma de trabajar en cada uno.
Esta entrada va dedicada a mis 51 alumnos de Cálculo Diferencial e Integral que comienzan semestre el próximo lunes. Bienvenidos al curso.
Diversas formas de ver un límite que no son propiamente matemáticas
 Un límite puede entenderse como una línea real o imaginaria que separa dos espacios (casas, ciudades, terrenos, etc).
Un límite puede entenderse como una línea real o imaginaria que separa dos espacios (casas, ciudades, terrenos, etc).
No, el límite que aprenderemos a determinar hoy no siempre es una línea, más bien es un valor (cuando existe).
Un límite puede verse como el final o el extremo de algo (fecha límite, límite del estacionamiento, límite de la paciencia, etc.).
No, nuestro límite no siempre es el final de algo.
 Un límite puede verse como una restricción (límite de velocidad, límite de ocupantes en un elevador).
Un límite puede verse como una restricción (límite de velocidad, límite de ocupantes en un elevador).
No, al determinar un límite como los que veremos hoy no obtenemos un valor como esos, que restringen pero pueden no respetarse.
¿Qué es entonces un límite en matemáticas?
Existen diversas formas de entender los límites en matemáticas:
Límite de una sucesión:
Es el número al que se van acercando los términos de una sucesión. Puede o no existir. Escribiré sobre eso en otra ocasión.
Límite de una función:
Es el valor al que tiende la función cuando la variable independiente tiende a un valor dado, sin tomar ese valor.
¿Por qué un concepto que se puede resumir en esa frase tan inocente es tan elusivo de aprender?
Algunas dificultades relacionadas con la comprensión del concepto de Límite
Además de las diversas formas de ver un límite que acabamos de revisar, que fomentan la confusión de conceptos, existen otras dificultades que listaré a continuación.
Forma de determinar diferente a la usada en otros contextos
 Una razón de la dificultad para comprender este tema es que el determinar un límite implica revisar qué ocurre al acercarse a un valor por ambos lados, lo cual no es tan fácil de relacionar con los conceptos de límite que normalmente manejamos, como un límite de capacidad de un contenedor, por ejemplo. Si lo excedes, se tira lo que estés agregando. El límite en cálculo es diferente.
Una razón de la dificultad para comprender este tema es que el determinar un límite implica revisar qué ocurre al acercarse a un valor por ambos lados, lo cual no es tan fácil de relacionar con los conceptos de límite que normalmente manejamos, como un límite de capacidad de un contenedor, por ejemplo. Si lo excedes, se tira lo que estés agregando. El límite en cálculo es diferente.
Decisiones pedagógicas
 Sin pretender generalizar, sólo basada en lo que he visto y vivido, creo que otra razón puede ser que se le dedica poco tiempo dentro del programa de la materia de Cálculo Diferencial e Integral a ver este tema. La determinación de un límite es la base para obtener derivadas e integrales, sin embargo, en la mayoría de los casos existen caminos más cortos para obtenerlas, así que los profesores podemos caer en la tentación de ver “por encima” este tema y después concentrarnos en enseñar a derivar e integrar, olvidando por completo la determinación de límites, hasta el examen final.
Sin pretender generalizar, sólo basada en lo que he visto y vivido, creo que otra razón puede ser que se le dedica poco tiempo dentro del programa de la materia de Cálculo Diferencial e Integral a ver este tema. La determinación de un límite es la base para obtener derivadas e integrales, sin embargo, en la mayoría de los casos existen caminos más cortos para obtenerlas, así que los profesores podemos caer en la tentación de ver “por encima” este tema y después concentrarnos en enseñar a derivar e integrar, olvidando por completo la determinación de límites, hasta el examen final.
Con tanto material por aprender, los propios alumnos pueden restarle importancia a estudiar los límites y esto hace que el problema crezca. No lo enseñamos bien, no lo aprenden bien y nadie sale demasiado afectado por ello, ¿para qué molestarse por buscar alternativas? Se vuelve un círculo vicioso: si muchos le dan poca importancia al tema, pocos se preocupan por analizar cómo lograr entender para sí y luego que los otros entiendan este tema.
Confieso que eso me pasó al principio de mi aventura de enseñar Cálculo, hace quince años. Empezó el ciclo escolar, enseñé lo mejor que pude el tema de límites, hasta donde lo entendía. No creo que mis alumnos me hayan entendido del todo, pero nadie reprobó por eso, así que mi conciencia no me dio mucha lata. Pero resulta que soy alguien a quien le gusta entender el porqué de las cosas… y compartirlo, que es la esencia de este blog, así que eso es lo que haré en este par de entradas, compartir lo que he logrado entender del tema desde entonces hasta hoy.
Comprensión de los conceptos de cero e infinito
 Además, el obtener límites implica entender bien cómo trabajar con el cero y el infinito, que, como aparecieron hace relativamente poco en la matemática, todavía no nos sentimos del todo cómodos en su presencia. El cero, si bien es un número, tiene peculiaridades que ningún otro número tiene: no tiene signo, no es posible dividir entre cero, etc. (ver más sobre el cero aquí). El infinito no es número, pero es un concepto indispensable para determinar y entender algunos límites interesantes.
Además, el obtener límites implica entender bien cómo trabajar con el cero y el infinito, que, como aparecieron hace relativamente poco en la matemática, todavía no nos sentimos del todo cómodos en su presencia. El cero, si bien es un número, tiene peculiaridades que ningún otro número tiene: no tiene signo, no es posible dividir entre cero, etc. (ver más sobre el cero aquí). El infinito no es número, pero es un concepto indispensable para determinar y entender algunos límites interesantes.
 A propósito, en la determinación de los límites, el cero y el infinito tienen una fuerte relación. Si se divide una cantidad entre un número de partes muy grande, que se acerca a infinito, cada parte tendrá un valor muy pequeño, esto es, un valor que se acerca a cero. En cambio, si se divide una cantidad entre un número muy pequeño, que se acerca a cero, se obtendrá una cantidad muy grande, que se acerca a infinito.
A propósito, en la determinación de los límites, el cero y el infinito tienen una fuerte relación. Si se divide una cantidad entre un número de partes muy grande, que se acerca a infinito, cada parte tendrá un valor muy pequeño, esto es, un valor que se acerca a cero. En cambio, si se divide una cantidad entre un número muy pequeño, que se acerca a cero, se obtendrá una cantidad muy grande, que se acerca a infinito.
Por eso algunos autores señalan que al dividir un número diferente de cero entre cero el resultado es infinito y al dividirlo entre infinito el resultado es cero. Expresarlo así es impreciso. Es mejor expresarlo con tendencias. Lo veremos con más detalle la próxima semana.
Comprensión del concepto de función
Para obtener el límite de una función, es necesario tener muy claro lo que es una función. Y para ello necesitamos comprender los conceptos de variable independiente y dependiente. Ah, muy cierto, también necesitamos saber cómo determinar el dominio de una función.
Presento aquí brevemente esos conceptos, dado que los necesitaremos en adelante. En una entrada posterior los profundizaré:
Una función es una regla que asigna a cada elemento del conjunto de entrada (el conjunto de valores de la variable independiente, normalmente identificada como x) máximo un elemento del conjunto de salida (el conjunto de valores de la variable dependiente, normalmente identificada como y)
El dominio de la función es el conjunto de valores de la variable independiente (x) para los cuales la función está definida, es decir, se puede calcular la variable dependiente (y) mediante la función.
La clave para entender el dominio está en la palabra “definida”. Sólo pueden formar parte del dominio aquellos valores de x con los que se puede calcular y. Un ejemplo sencillo es este:
 La función que relaciona un valor con su inverso es:
La función que relaciona un valor con su inverso es:
y = 1/x
Su dominio son todos los valores de x que permiten calcular y, por lo que son todos los números reales menos el cero, ya que no es posible dividir entre cero.
¿Qué otras dificultades para la comprensión del concepto de límite conocen?
Notación (forma de escribir un límite)
El límite de la función f(x) cuando x tiende a a, es L. Se escribe:
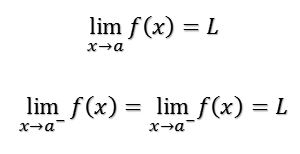
Para que el límite exista, debe ser igual por ambos lados, que es la condición escrita abajo.
Determinación gráfica de un límite
Considero que observar lo que ocurre con una gráfica ayuda a comprender el significado del límite. Observen esta gráfica:

Ahora llenemos esta tabla. En la primera columna van los valores de la variable independiente. Noten los signos que están arriba a la derecha de algunos números Indican la lateralidad del límite: menos, izquierda, más, derecha. Si no tiene el signo, sólo podemos poner un valor en la tabla si los límites son iguales por ambos lados.

Veamos la tabla llena. Pueden notar que, cuando x tiende a menos infinito, la función tiende a 2, pero está por abajo del 2. En cambio, cuando la función tiende a más infinito. la función también tiende a 2, pero está por arriba de 2. Se trata de una asíntota horizontal a ambos lados.
Por otro lado, cuando x tiende a 0, tanto por izquierda como por derecha, la función tiende a 1, por lo tanto, el límite de la función cuando x tiende a 0 es 1. Finalmente veamos lo que pasa cuando x tiende a 1. Por la izquierda, la función tiende al infinito negativo, por la derecha, tiende al infinito positivo. Son diferentes, por tanto, el límite de la función cuando x tiende a 1 no existe.

Así se vería en notación de límites:

Determinación de un límite por aproximaciones sucesivas
Ahora determinaremos un límite a partir de una función conocida, sin tener su gráfica. Usaremos esta función racional, que tiene una estructura que ayuda a entender algunos aspectos relevantes de los límites:

¿A qué valor tiende esa función cuando x tiende a 3, sin ser 3?
Bueno, si x no puede ser 3, entonces podemos calcular el valor de la función con números cercanos (menores y mayores) a 3:

¿Observan lo que pasa? El valor al que tiende, por ambos lados, es 6.
¿Y si nos ponemos rebeldes y calculamos el valor de la función justo en 3? Observen lo que pasa:

La sustitución nos lleva a un 0/0, es decir, una respuesta indeterminada (que NO es lo mismo que indefinida, en la que el valor del numerador es diferente de cero). El obtener un resultado indeterminado significa que, probablemente con un poco de trabajo extra podemos lograr determinar el valor al que tiende esa función cuando x tiende a 3, o darnos cuenta de que está indefinido. Esas tabulaciones que hicimos son una forma de hacer ese trabajo extra, pero no es la única.
De hecho, cuando se enseña límites, normalmente se hacen sólo uno o dos ejercicios con tabulaciones como éste para comprender la idea y después se continúa con una determinación basada en manipulaciones algebraicas, como veremos más adelante.
Veamos cómo se escribe el límite anterior:

Por lo tanto, el límite de la función cuando x tiende a 3, es 6. Recuerden que obtuvimos 6 tanto con valores más pequeños como con valores más grandes, por lo que el límite sí existe, aunque la función esté indeterminada en x=3. Los límites se determinan cuando la variable independiente tiende a cierto valor, NO cuando está en ese valor.
¿Sustituir o no sustituir?
Es muy importante entender que el límite es un valor que no se alcanza nunca, dado que el valor de x no se alcanza nunca, pero que es bastante cercano al último valor que se alcanzaría.
 Sin embargo un alto porcentaje de alumnos llega a la universidad diciendo que los límites se determinan sustituyendo. ¿Por qué pasa eso?
Sin embargo un alto porcentaje de alumnos llega a la universidad diciendo que los límites se determinan sustituyendo. ¿Por qué pasa eso?
Porque existen ciertas propiedades o teoremas que hacen que, para efectos prácticos, el procedimiento más rápido para obtener el límite de una función polinómica (y de muchas otras lejos de los valores que pueden provocar conflicto) sea la sustitución.
Personalmente creo que es válido hacerlo, pero recordando siempre que es posible hacer esa sustitución por las propiedades de los límites, no porque ese sea el procedimiento para determinar un límite. Estos son unos ejemplos de esas propiedades:

Para cerrar
 Hace poco me hicieron ver esta diferencia entre complejo: una situación que tiene muchas partes o aspectos y complicado: cuando no logramos distinguir esas partes y, por tanto, no sabemos qué hacer en esa situación. Confío en que, con lo que estamos revisando sobre los límites, éstos dejen de ser complicados y pasen a ser solo complejos, con muchos aspectos que sí entendemos y, por tanto, podemos atender.
Hace poco me hicieron ver esta diferencia entre complejo: una situación que tiene muchas partes o aspectos y complicado: cuando no logramos distinguir esas partes y, por tanto, no sabemos qué hacer en esa situación. Confío en que, con lo que estamos revisando sobre los límites, éstos dejen de ser complicados y pasen a ser solo complejos, con muchos aspectos que sí entendemos y, por tanto, podemos atender.
Los dejaré en suspenso sobre cuáles son los diferentes casos que nos podremos encontrar al determinar los límites de funciones. Nos leemos la próxima semana para terminar de revisar este tema. ¿Saben? Por casualidades del destino, esta entrada se publicó a pocos minutos de que se terminara el miércoles. Espero la próxima semana sí publicar temprano.
Como siempre, gracias por leer, por aprender, por enseñar, por compartir, por comentar, por disfrutar y por difundir el mensaje.
Un abrazo
Rebeca
PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.
PD2: Quiero agradecer a estas páginas en las que me apoyo constantemente para redactar el blog: pixabay y webresizer
Obtuve parte de esta información de Wikipedia, del Diccionario de la Real Academia de la Lengua y del libro Matemáticas para administración y economía de Haeussler, Paul y Wood
Usé Word y Geogebra para hacer las imágenes


Hace mucho tiempo que esperaba » comprender » y no solo » saber » como calcular Limites; por casualidad llegué hasta aquí y simplemente quisiera dejar constancia de mi agradecimiento a personas como tu por divulgar en forma tan clara y precisa el conocimiento. ¡ gracias por iluminarme!
Me gustaMe gusta
¡Muchas gracias por tu comentario, Omar!
Me gustaMe gusta
Wow, acabo de entender mucho más que en otros sitios, es bastante explícito y eso lo hace único.
¡Graciaaass¡… 😊🤗
Me gustaLe gusta a 1 persona
Me da mucho gusto leer que te resultó útil, Ubaldo.
Gracias por dejar tu comentario 🙂
Me gustaMe gusta
Muy buena explicacion muchas gracias me ha ayudado mucho
Me gustaMe gusta
¡Gracias!
Me gustaMe gusta
[…] más sobre límites aquí y […]
Me gustaMe gusta
[…] en la actualidad se estudia usando límites (ver más sobre límites aquí y aquí). Incluso algunos cursos se saltan esta explicación y pasan directamente a las reglas que […]
Me gustaMe gusta
[…] ésta es la segunda entrada, de dos, dedicada al tema de límites de funciones. En la primera (ver aquí) revisamos las distintas formas de ver un límite, las dificultades para comprender adecuadamente […]
Me gustaMe gusta
Para ser sincero no esperaba que fuera así de explicativo el blog, lo imagine pesado y tedioso.
Pero que buena sorpresa me lleve.
¡Gracias!
Me gustaLe gusta a 1 persona
Me da mucho gusto haberte sorprendido gratamente, Juan Carlos.
Todo el concepto del blog está enfocado en buscar que la gente mejore su relación con las matemáticas y una forma de lograrlo es explicando las cosas de una forma que sea matemáticamente correcta, pero a la vez fácil de entender, aprender y enseñar.
Gracias a ti por darte el tiempo de escribir un comentario.
Me gustaMe gusta