Ésta es la entrada número 53 de este blog. Dado que un año no bisiesto tiene 52 semanas y un día, las probabilidades de que fuera la primera entrada del segundo año de vida del blog serían, en teoría, de 6/7. Sin embargo, no lo es. Esa y otras peculiaridades que ocurren con los días de la semana, los años de nuestra era, etcétera, serán el tema de esta entrada.
 Pregunta: Si quisiéramos tener un calendario como el de la imagen para cada uno de los diferentes años que pueden existir, sin importar si se trata de 1991 o 2019, ¿cuántos diferentes tendríamos? Sigan leyendo, para que puedan conocer los patrones presentes en el calendario. lo que ayuda a desarrollar el pensamiento lógico (ver más aquí, aquí y aquí) y a saber la respuesta.
Pregunta: Si quisiéramos tener un calendario como el de la imagen para cada uno de los diferentes años que pueden existir, sin importar si se trata de 1991 o 2019, ¿cuántos diferentes tendríamos? Sigan leyendo, para que puedan conocer los patrones presentes en el calendario. lo que ayuda a desarrollar el pensamiento lógico (ver más aquí, aquí y aquí) y a saber la respuesta.
Dedico esta entrada a la Dra. Elena Nesterova, mi directora de tesis de la maestría y la única persona que conozco que cumple años el 29 de febrero. ¿Habrá celebrado su cumpleaños número 15 el año que sus compañeras de clases estaban celebrando su cumpleaños número 60?Leer más »




 Existen muchos libros que fueron escritos con este objetivo: la divulgación de la matemática fuera del contexto escolar. Comentaré aquí sobre aquellos que conozco, he leído y me han gustado y también sobre los que espero leer pronto. Agradeceré que en los comentarios nos compartan otros títulos que ustedes conozcan de este estilo.
Existen muchos libros que fueron escritos con este objetivo: la divulgación de la matemática fuera del contexto escolar. Comentaré aquí sobre aquellos que conozco, he leído y me han gustado y también sobre los que espero leer pronto. Agradeceré que en los comentarios nos compartan otros títulos que ustedes conozcan de este estilo.
 La idea de esta entrada surgió al ver la sudadera que traía mi hijo David, con un gran número 19 escrito en romano: XIX. Se trata de un capicúa, o número palíndromo, esto es, que se lee igual de izquierda a derecha y de derecha a izquierda. Incluso se lee igual si se le pone de cabeza. El verlo me hizo querer averiguar cuántos otros capicúas habría entre los números romanos. Sospechaba que serían muy pocos, lo cual confirmé mediante el pequeño análisis que les presento hoy. De verdad que era limitada esa numeración, por ello la matemática estuvo detenida en Europa hasta que llegó la numeración indo-arábiga, que es posicional (ver más sobre el sistema numérico decimal
La idea de esta entrada surgió al ver la sudadera que traía mi hijo David, con un gran número 19 escrito en romano: XIX. Se trata de un capicúa, o número palíndromo, esto es, que se lee igual de izquierda a derecha y de derecha a izquierda. Incluso se lee igual si se le pone de cabeza. El verlo me hizo querer averiguar cuántos otros capicúas habría entre los números romanos. Sospechaba que serían muy pocos, lo cual confirmé mediante el pequeño análisis que les presento hoy. De verdad que era limitada esa numeración, por ello la matemática estuvo detenida en Europa hasta que llegó la numeración indo-arábiga, que es posicional (ver más sobre el sistema numérico decimal 

 De entre las figuras geométricas básicas que existen: cuadrado, triángulo, rectángulo, círculo…, el círculo posee características que lo hacen muy diferente a las demás, empezando porque se necesita un compás para dibujarlo, a comparación de las que se dibujan con regla (bueno, también se pueden dibujar a mano alzada, como en la imagen, pero no quedan tan bien).
De entre las figuras geométricas básicas que existen: cuadrado, triángulo, rectángulo, círculo…, el círculo posee características que lo hacen muy diferente a las demás, empezando porque se necesita un compás para dibujarlo, a comparación de las que se dibujan con regla (bueno, también se pueden dibujar a mano alzada, como en la imagen, pero no quedan tan bien).
 La entrada pasada, que pueden ver
La entrada pasada, que pueden ver 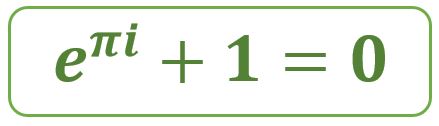
 Publico esta entrada un 14 de marzo, conocido en el mundo de las matemáticas como el día de pi (π), por escribirse la fecha en algunos países como 3.14. Esta coincidencia me llevó a elegir escribir sobre pi y otros números especiales.
Publico esta entrada un 14 de marzo, conocido en el mundo de las matemáticas como el día de pi (π), por escribirse la fecha en algunos países como 3.14. Esta coincidencia me llevó a elegir escribir sobre pi y otros números especiales.