Ideas para aplicar en bachillerato
En la entrada pasada (ver aquí) vimos la diferencia entre sucesión, serie y patrón de formación, conocimos algunas formas de iniciar a los niños en las sucesiones y también cómo encontrar un término de una sucesión a partir del patrón de formación. En ésta veremos el proceso inverso, es decir, cómo determinar el patrón de formación de una sucesión de números. Aprovecharemos para ver lo que son las progresiones, así como algunas características de las series.Leer más »
Se dice que las matemáticas son la ciencia de los patrones. Algunos son sencillos de reconocer, otros son más “truculentos”, por decirlo de alguna manera. Cuando se trabaja con sucesiones y series, se reconocen patrones, por eso es tan importante hacerlo. 
Escribiré, en esta entrada y en la siguiente, tanto sobre las sucesiones y series más sencillas, como sobre algunas más complejas, para que todos los profesores y papás con hijos en distintos niveles escolares encuentren algo útil y, lo más importante, entiendan de dónde viene y hacia dónde va este tema. Recuerden la importancia de las conexiones entre conocimientos.
Esta entrada va dedicada a Mely, una entusiasta profesora de primaria que me sugirió el tema. Gracias por ello.Leer más »
Los profesores y los papás hacemos preguntas a nuestros alumnos e hijos y esperamos provocar en ellos un proceso de pensamiento (como fichas de dominó que caen una tras otra, o como algo más complejo) que los lleven a ciertas respuestas. Para algunas preguntas, las respuestas pueden obtenerse y/o expresarse de diferentes formas. Según la intención didáctica de la pregunta (lo que queremos que aprendan al contestarla), puede ser necesario que sea respondida de cierta forma y/o con cierto proceso. Sobre eso compartiré algunas ideas hoy.
Se me ocurrió escribir acerca de esto al ver cómo calificó la maestra una tarea de fracciones de mi sobrino, en quinto de primaria. Los valores de las respuestas estaban bien calculados, pero al parecer no estaban expresados como ella esperaba, así que llenó de “taches” la hoja, sin que el niño comprendiera del todo por qué. Sigan leyendo para conocer el resto de la historia.Leer más »
Ésta es la entrada número dieciocho de este blog. Dieciocho es dos veces nueve, que es un número que me encanta (ver sus características en la novena entrada, aquí), así que corresponde hacer algo especial.
Hoy compartiré algunas ideas que pueden ayudar a desarrollar el pensamiento lógico matemático en personas de todas las edades. Expliqué en la segunda entrada del blog (ver aquí) que lo considero el primer pilar de una buena relación con las matemáticas y que, para mí, el segundo pilar es el sentido numérico (ver aquí).
Como no es posible desarrollar el pensamiento lógico matemático en algunas clases sueltas a lo largo del ciclo escolar, porque sería un aprendizaje raro, descontextualizado y poco duradero, necesita trabajarse un poco en cada clase o en cada interacción con nuestros hijos. Revisemos algunas ideas para hacerlo y veamos cómo es útil más allá de las actividades escolares.Leer más »
En la entrada pasada (ver aquí) escribí sobre qué es una ecuación, para qué sirve, qué significa resolverla, cuántas soluciones tiene, qué cuidados es necesario tener al resolverla, cuáles son las operaciones con las que se resuelve, por qué es importante entender la solución de ecuaciones de la forma correcta y concluí con una idea para iniciar a los niños de primaria en el álgebra… Vaya, a veces alcanzo a compartir mucha información en una sola entrada. Lo bueno es que ustedes pueden tomarse el tiempo que necesiten para leerla y hacerla suya. La información se queda ahí para cuando requieran consultarla.
Esta entrada es un complemento a la anterior, describo con más detalle algunos conceptos y proporciono más estrategias para solucionar ecuaciones lineales con una incógnita (como un mapa y una brújula para «encontrar el valor de x«). Incluí una sección con ideas para construir ecuaciones lineales con una incógnita que sean interesantes de resolver (digamos que son instrucciones para «esconder el valor de x«).Leer más »
En la entrada sobre sentido de estructura (ver aquí) escribí, entre otras cosas, sobre cómo se conforman las estructuras algebraicas y sobre los significados del signo igual, según el tipo de estructura algebraica dentro de la cual se encuentra.
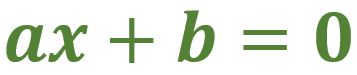
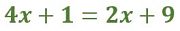Ahora escribiré sobre lo que es una ecuación, lo que significa “resolver una ecuación” y los cuidados que son necesarios al “resolver una ecuación lineal con una incógnita”. También incluiré una sugerencia sobre cómo plantear ejercicios en primaria que preparen a los alumnos para resolver ecuaciones lineales en secundaria.Leer más »
En la entrada anterior (ver aquí) presenté tres estrategias para aprender y practicar las tablas de multiplicar. Una basada en observación de patrones, otra en tarjetas y una más en la vida diaria. En ésta presentaré más estrategias para que todos lleguemos a dominar las tablas al derecho y al revés. Eso de verdad hará una gran diferencia en nuestras vidas, nos abrirá la puerta a conocimientos matemáticos a los que no podíamos acceder por falta de esa habilidad. ¿Cómo podría alguien dividir dos números de 3 cifras, sacar raíces cuadradas o factorizar un trinomio sin saberse las tablas de multiplicar?Leer más »
Elijo lo que voy a escribir basándome en lo que veo importante compartir, según las dificultades que observo en mis hijos y alumnos, y lo que me comentan profesores, papás y lectores del blog. Me he dado cuenta de que las tablas de multiplicar son uno de esos temas que es muy importante compartir.
En la tercera entrada, sobre sentido numérico (ver aquí), comenté por qué es importante ser creativo y flexible al hacer operaciones numéricas, lo cual implica conocer a profundidad las tablas de multiplicar. 
En esta entrada y en la de la próxima semana compartiré algunas ideas que pueden servir para que esas elusivas tablas dejen de ser el enemigo y se conviertan en el aliado de los niños (y no tan niños) al enfrentar tareas matemáticas. Para que aquellos que aún no «se saben las tablas», vean una luz al final del túnel, mediante una forma diferente de acercarse a ellas. Leer más »
En la entrada pasada (ver aquí) vimos cómo elegir las medidas para crear distintos tipos de triángulos, que sí se pueden construir, con medidas enteras en su altura y sus lados. En esta conoceremos como hacer lo mismo con otras figuras geométricas: algunos cuadriláteros (rombos, romboides, trapecios) y polígonos regulares.Leer más »
IMPULSO MATEMÁTICO 