Se dice que las matemáticas son la ciencia de los patrones. Algunos son sencillos de reconocer, otros son más “truculentos”, por decirlo de alguna manera. Cuando se trabaja con sucesiones y series, se reconocen patrones, por eso es tan importante hacerlo.  Escribiré, en esta entrada y en la siguiente, tanto sobre las sucesiones y series más sencillas, como sobre algunas más complejas, para que todos los profesores y papás con hijos en distintos niveles escolares encuentren algo útil y, lo más importante, entiendan de dónde viene y hacia dónde va este tema. Recuerden la importancia de las conexiones entre conocimientos.
Escribiré, en esta entrada y en la siguiente, tanto sobre las sucesiones y series más sencillas, como sobre algunas más complejas, para que todos los profesores y papás con hijos en distintos niveles escolares encuentren algo útil y, lo más importante, entiendan de dónde viene y hacia dónde va este tema. Recuerden la importancia de las conexiones entre conocimientos.
Esta entrada va dedicada a Mely, una entusiasta profesora de primaria que me sugirió el tema. Gracias por ello.
¿Cuál es la diferencia entre sucesión, serie y patrón?
Primero lo primero, entendamos la diferencia entre los tres conceptos. Usemos un ejemplo muy sencillo:
Esto es una sucesión: 1, 3, 5, 7, 9
Esto es una serie: 1 + 3 + 5 + 7 + 9
En efecto, la diferencia está en que:
La sucesión es un conjunto de números u otros elementos (llamados términos) ordenados según un patrón o regla de formación.
La serie es un conjunto de números (llamados términos) ordenados según un patrón o regla de formación, unidos por una operación, comúnmente una suma.
Al estar los términos de la serie unidos por un operador, se puede calcular el valor de la serie. El del ejemplo sería 25. En cambio, la sucesión es simplemente una lista de elementos, no se puede calcular su valor.
El patrón o regla de formación, es lo que nos permite conocer cómo calcular cada término de la sucesión o de la serie a partir de la posición del mismo. Las posiciones empiezan en 1 regularmente.
 Confieso que me resultó confuso al principio el entender que una serie fuera una suma. Al reflexionar por qué, me di cuenta de que “serie” es una palabra que se usa en el español no-matemático para cosas que no son sumas: en México decimos que vemos una serie de televisión, que necesitamos el número de serie de un vehículo para asegurarlo, que una serie de contratiempos me impidió publicar esta entrada más temprano el día de hoy (verídico), etcétera.
Confieso que me resultó confuso al principio el entender que una serie fuera una suma. Al reflexionar por qué, me di cuenta de que “serie” es una palabra que se usa en el español no-matemático para cosas que no son sumas: en México decimos que vemos una serie de televisión, que necesitamos el número de serie de un vehículo para asegurarlo, que una serie de contratiempos me impidió publicar esta entrada más temprano el día de hoy (verídico), etcétera.
Por tanto, para poder trabajar con “series” en matemáticas, debemos estar conscientes de esta diferencia de significado. ¿Cómo se usará la palabra «serie» en otros lugares y contextos? Espero que los lectores de otros países nos apoyen dándonos esa información en los comentarios.
Algunos conceptos que necesitamos conocer antes de seguir
Los definiré aquí y se irán entendiendo mejor conforme se avance en la lectura.
Término: cada elemento de una sucesión. Suele identificarse con la letra a y un subíndice que empieza en el 1.
Término enésimo: el término a subíndice n, necesario para indicar el patrón de formación.
Patrón o regla de formación de una sucesión: fórmula que permite calcular el término enésimo de ciertas sucesiones, es decir, el valor del término en la posición n.
En el ejemplo anterior:
El patrón de formación indica que la posición del término (n) se multiplica por dos y se le resta uno para obtener su valor. El valor del término en la posición nueve será, por tanto, 2(9) – 1=17.
¿Todas las sucesiones son iguales?
Ya se imaginarán que no, ¿verdad?
Sucesiones sin patrón de formación expresado como fórmula
Hay sucesiones que tienen un patrón de formación que no puede redactarse como una fórmula matemática, pero que sí puede observarse y seguirse. Incluso algunas no tienen números.
Veamos ésta:
A, C, E, G…
¿Qué elemento sigue? La letra I, porque el patrón de formación indica que se escribe una letra sí y otra no del abecedario.
Ahora ésta, que incluye números, pero que no se usa propiamente una fórmula, sino un proceso para formarla:
12358, 23581, 35812, 58123…
Puede observarse cómo el primer número en un término pasa a ser el último número en el siguiente término y todos se recorren a la izquierda. Lo mismo para cada nuevo término.
Y esta otra que me parece muy interesante:
1, 11, 21, 1211, 111221
El patrón formación de esta sucesión, aunque los términos sean números, tampoco puede redactarse como una fórmula matemática. ¿Cuál sería el siguiente término? Observen con cuidado para poderlo determinar. Les daré la respuesta antes de cerrar esta entrada.
Sucesiones con patrón de formación expresado como fórmula
También están las sucesiones para las que sí se puede redactar el patrón de formación como una fórmula matemática, como las siguientes.
Sucesiones aritméticas, polinomiales lineales o de primer orden (tres nombres diferentes para el mismo tipo de sucesión): la diferencia entre un término y el siguiente es un valor constante, como en:
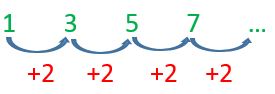
1, 3, 5, 7…
Se puede observar que, para llegar de un valor al siguiente, se le suma 2 al primer valor, partiendo del número 1. Eso se traduce en un patrón de formación según el cual se multiplica por 2 la posición del término y se le resta uno, como vimos antes.

Sucesiones polinomiales cuadráticas o de segundo orden: la segunda diferencia entre un término y el siguiente es un valor constante, como en:
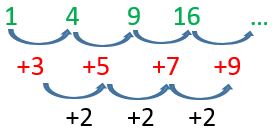
1, 4, 9, 16…
Puede observarse que, para llegar de un valor al siguiente, se le suma un número que también va creciendo. Si se saca la segunda diferencia, se observa que ese número ya es constante: 2. Cuando la segunda diferencia es constante, se trata de una sucesión de segundo grado. Se traduce, en este caso, en un patrón de formación según el cual la posición del término debe elevarse al cuadrado.
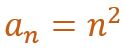
Los patrones de formación de sucesiones cuadráticas pueden ser más complejos que éste, como veremos adelante.
También hay sucesiones de orden superior a dos. En las de orden tres, la tercera diferencia entre un término y el siguiente es un valor constante y así sucesivamente.
Sucesiones geométricas: la razón (división) entre un término y el siguiente es un valor constante, como en:
2, 4, 8, 16…
Aquí se puede observar que, para llegar de un valor al siguiente, se multiplica por dos el primer valor, partiendo del 2. Visto de otra manera, al dividir cada término entre el anterior a él se obtiene un valor constante, 2. Eso se traduce en un patrón de formación según el cual se 2 se eleva a un número que es la posición del término.
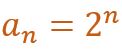
Las series pueden tener patrón de formación expresado como fórmula, veremos la forma de expresarlo en la siguiente entrada.
Comportamiento de las sucesiones
Por su comportamiento, las sucesiones pueden considerarse

 Sucesiones ascendentes o crecientes: cada nuevo término es mayor al anterior.
Sucesiones ascendentes o crecientes: cada nuevo término es mayor al anterior.
Sucesiones descendentes o decrecientes: cada nuevo término es menor al anterior.
 Sucesiones alternadas: los términos se alternan, ya sea que uno crezca y el siguiente decrezca o que uno sea positivo y el siguiente negativo, o ambos cambios a la vez.
Sucesiones alternadas: los términos se alternan, ya sea que uno crezca y el siguiente decrezca o que uno sea positivo y el siguiente negativo, o ambos cambios a la vez.
Las series también se clasifican según su comportamiento. También lo veremos en la siguiente entrada. Veamos ahora algunas ideas para practicar con las sucesiones.
Iniciación a las sucesiones
Para enseñar a reconocer patrones, puede empezarse con imágenes que se repitan en un cierto orden. No es precisamente una sucesión, pero ayuda a entenderlas posteriormente. ¿Cuál es la figura que sigue?

Sigue… un triángulo morado con la punta hacia abajo.
También se puede hacer con algo físico, como dulces o cereal de colores que se pueda ensartar. Así se cumple una doble función con la actividad: practican psicomotricidad fina y también a seguir patrones:

Más adelante se pueden usar unas imágenes que ya sean propiamente una secuencia, en las que se puede intuir la figura que sigue por la forma y el conteo de cuadritos.
Ésta es una secuencia polinomial lineal, dado que la cantidad de cuadritos va aumentando con una diferencia constantes: 3, 5, 7, 9… sigue el 11.
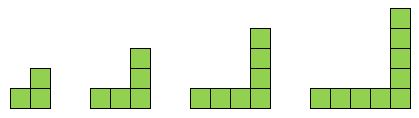
En cambio, ésta es una secuencia polinomial cuadrática, dado que la cantidad de cuadritos va aumentando con una diferencia que también aumenta: 1, 3, 6, 10… sigue el 15.
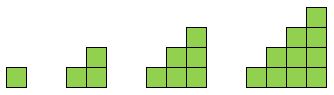
Como dato curioso: a esos números: 1, 3, 6, 10… se les llama triangulares, por su forma de triángulo al representarse así acomodados. Tienen, además, una característica interesante: si sumamos dos números triangulares consecutivos, obtenemos un número cuadrado. Se puede visualizar si se voltea el triángulo pequeño y se acomoda junto al grande, así:

Después de las imágenes sin y con relación con los números, se puede empezar con algo numérico:
2, 4, 6, 8, 10…
Sigue: el 12
Es común que se practiquen las sucesiones de los primeros 10 o 12 números como una forma de preparación para las tablas:
3, 6, 9, 12…
7, 14, 21, 28…
Creo que hacerlo es de ayuda, siempre y cuando llegue el momento en que se separe la tabla de multiplicar de la sucesión, para poder usar las tablas más eficientemente, sin ningún orden específico.
Considero que es una buena idea que, además de calcular la diferencia entre cada par de términos y usarla para calcular el siguiente término, les pidamos a nuestros hijos y alumnos que escriban abajo, en medio de cada par de números, esa diferencia.
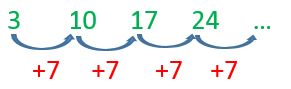
Creo que eso remarca la idea de que es un ejercicio diferente a escribir el número siguiente del último que ven (algo que hacen cuando no ponen el suficiente cuidado, probablemente sólo ven con atención el último número y no los demás). Al ver las flechas y los números abajo, es más factible que “desconecten el contestador automático” y analicen con más calma cuál debería ser la respuesta.
Se puede variar el ejercicio dejando como desconocido el primer valor:

O uno intermedio:

Se puede ser muy creativo al presentar las sucesiones a los alumnos, insertándolas en dibujos, en historias, etc.
Obtener un término a partir del patrón de formación
Es muy sencillo, sólo se sustituye el número del término dentro de la fórmula. Veamos cómo obtener el primero, el quinto y el décimo términos de las siguientes sucesiones:
Esta es una sucesión de primer orden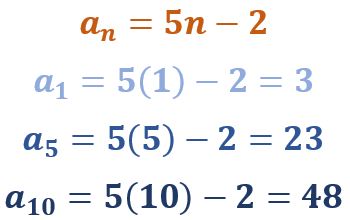
Esta es una sucesión de segundo orden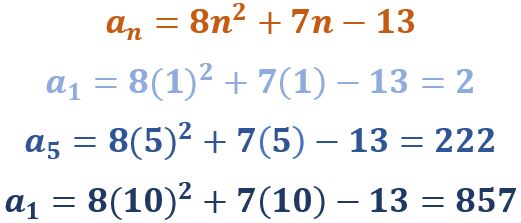
Y esta es una sucesión geométrica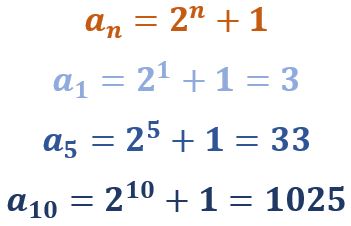
¿Observan la velocidad a la que crecen los términos? Para todas el primer término es 3, sin embargo, el décimo término de la primera es 48, el de la segunda es 857 y el de la tercera es 1025. Ya para el término número 100, la primera toma el valor de 498, la segunda toma el valor de 806 687 y la tercera toma un valor que empieza en 1 y tiene ¡30! dígitos más. Como vemos, las geométricas pueden crecer muy rápidamente… o decrecer muy ¿lentamente?, como en este caso, en el que cada nuevo valor está más cerca del 1:
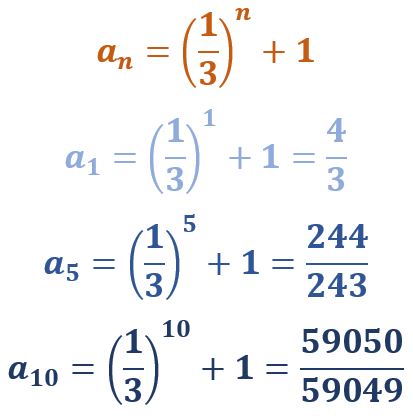
La próxima semana escribiré sobre el proceso inverso, esto es, cómo obtener el patrón de formación correspondiente a una secuencia de números. También un poco sobre series y sobre algunas curiosidades más de este tema tan interesante.
Para cerrar
¿Por qué escribí en el título de esta entrada que los patrones, sucesiones y series nos ayudan a interpretar al mundo? Porque el identificar patrones y usarlos para determinar qué sigue, nos sirve para volvernos hábiles para interpretar lo que ocurre conforme algo avanza y eso es muy útil fuera de la escuela, como lo expliqué en las entradas sobre pensamiento lógico-matemático, que pueden ver aquí y aquí.
 Por ejemplo, en un cruce con cuatro semáforos que se ponen en verde de forma individual, podemos observar el patrón que siguen para ponerse en verde (el que sigue a la derecha, por ejemplo) e identificar cuánto falta para que nos toque verde a nosotros. El cobro de ciertos servicios también sigue un patrón, con una tarifa básica y un incremento según el consumo. Y así sucesivamente 🙂
Por ejemplo, en un cruce con cuatro semáforos que se ponen en verde de forma individual, podemos observar el patrón que siguen para ponerse en verde (el que sigue a la derecha, por ejemplo) e identificar cuánto falta para que nos toque verde a nosotros. El cobro de ciertos servicios también sigue un patrón, con una tarifa básica y un incremento según el consumo. Y así sucesivamente 🙂
Los patrones pueden observarse en un listado o fila de elementos, o en un espacio en donde hacia arriba y abajo, hacia un lado y otro, incluso en diagonal, pueda observarse cómo se repiten los elementos, como en la imagen que encabeza esta entrada, dedicada a Irma, que tanto me ha apoyado con este blog y a quien le encantan los faros.
Además, identificar los patrones de formación numéricos ayuda de forma importante a desarrollar el sentido numérico, tan importante para tener una buena relación con las matemáticas en general (ver más aquí).
No crean que lo olvidé, aquí está la explicación de cómo se forma el siguiente término de la sucesión especial que les mostré anteriormente:
1, 11, 21, 1211, 111221 el siguiente es 312211
 Esta sucesión se conoce como desintegración audioactiva, ya que se forma diciendo lo que se ve en el término anterior, partiendo, en este caso de «un uno». Los siguientes términos serán, por tanto:
Esta sucesión se conoce como desintegración audioactiva, ya que se forma diciendo lo que se ve en el término anterior, partiendo, en este caso de «un uno». Los siguientes términos serán, por tanto:
un uno ⇒ dos unos ⇒ un dos un uno ⇒ un uno un dos un uno ⇒
tres unos dos doses un uno
Simpática la sucesión, ¿verdad?
Como siempre, gracias por leer y compartir con aquellos a quienes consideren que les pueda ser útil lo que aquí publico. Por favor, escríbanme si tienen alguna duda y si quieren sugerirme temas que deseen que aborde en futuras entradas del blog. Esperamos noticias sobre el uso de la palabra «serie» en otros países.
Nuevamente gracias por la sugerencia de tema, Mely, espero que te sirva más de alguna de las ideas que compartí.
Rebeca
PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.
PD2: Quiero agradecer a estas dos páginas en las que me apoyo constantemente para redactar el blog: https://pixabay.com/ http://webresizer.com/
La información sobre la desintegración audioactiva la obtuve de wikipedia. Hice algunas imágenes en Word y en Excel




tengo una duda con un ejercicio es buscar la formula para determinar el patron al multiplicar el valor del resultado anterior por 2, partiendo que 1=3,
2=6, 3=12, 4=24 y sucesivamente.
Me gustaMe gusta
Buen día, Pedro,
Por un lado cada nuevo término resulta de multiplicar por 2 el anterior, pero el primer factor debe ser 1 porque el primer valor no es par, por lo que la base del patrón es 2^(n-1)
Como el primer término es 3, ese valor necesita multiplicar al patrón.
Por lo tanto el patrón queda:
x_n = 2^(n-1) *3
Comprobando:
x_1 = 2^(1-1) *3 =3
x_2 = 2^(2-1) *3 =6
x_3 = 2^(3-1) *3 =12
x_4 = 2^(4-1) *3 =24
Espero que mi explicación haya sido suficientemente clara.
Saludos!
Me gustaMe gusta
Muchas gracias, me quedo clarito
Me gustaMe gusta
Con gusto. Saludos
Me gustaMe gusta
[…] la entrada que más vistas tiene en este blog, 207 804 en el momento en que escribo esto, se llama Sucesiones, series y patrones: nos ayudan a interpretar al mundo. Junto con la siguiente, Sucesiones y series: ¿cómo determinar el patrón de formación?, fueron […]
Me gustaMe gusta
[…] de este blog que han tenido más vistas son las dedicadas a sucesiones, series y patrones (ver más aquí y […]
Me gustaMe gusta
Pues hay que practicarlo porque esta muy interesante
Me gustaLe gusta a 1 persona
¡Muchas gracias!
Me gustaMe gusta
Hola respondiendo a la pregunta de Herry , yo decifro que el siguiente término de la sucesión 2,10,12,16,17,18,19, es 27
Me gustaMe gusta
quiero saber para que sirven las sucesiones aritméticas
en la vida cotidiana
Me gustaMe gusta
Hola, Camila,
Las sucesiones permiten identificar cómo se comporta «algo» y las aritméticas son muy parecidas a una función lineal, por lo que, sabiendo al menos dos elementos de la sucesión, podemos conocerla completa y saber qué dato corresponde al enésimo término.
Por ejemplo, si un taxista te dice que cobra una cuota fija, más una variable por kilómetro recorrido, pero por la prisa no alcanzas a escuchar cuánto por cada cosa, al observar que al recorrer un kilómetro el costo marcaba $12 y al recorrer dos kilómetros marcaba $14, eso es suficiente para identificar que la cuota fija es $10, la variable es $2 y recorrer los 15 kilómetros de tu viaje te costará $10+$2*15=$40.
Me gustaMe gusta
[…] caso, y las series son una suma de números. Pueden ver más sobre sucesiones, series y patrones aquí y sobre cómo encontrar el patrón de una sucesión o una serie […]
Me gustaMe gusta
[…] Mely, que me solicitó escribir sobre sucesiones series y patrones (ver aquí). Fue la primera entrada que escribí a petición de alguien y es la entrada que más vistas ha […]
Me gustaMe gusta
[…] Sucesiones, series y patrones: nos ayudan a interpretar al mundo (ver aquí) […]
Me gustaMe gusta
Para la sucesión 2, 10, 12, 16, 17, 18, 19.
La variación sería 8, 2, 4, 1, 1 y 1, por tanto, el octavo término sería 27.
Para la sucesión 2, 12, 17, 19.
La variación sería 10, 5 y 2, por tanto, el quinto término sería 29.
Para la sucesión 2, 10, 12, 16, 18.
La variación sería 8, 2, 4 y 2, por tanto, el sexto término sería 26.
Otra forma: es dividir cada uno de los términos de la sucesión por el primer término, entonces, la sucesión queda: 1, 5, 6, 8, 9. Luego, la variación sería: 4, 1, 2 y 1, por tanto el sexto término sería 13.
Me gustaMe gusta
Hola, Magaly,
Si se considera que las diferencias entre cada par de términos se reinician justo después de los términos que conocemos, tus respuestas son correctas: 19+8=27, 19+10=29, etc.
Otra forma de verlo es ésta: dos, diez, doce… todos empiezan con «d», por lo tanto, el siguiente término sería: doscientos.
El siguiente término de 2, 12, 17, 19 los números que empiezan con d, uno sí y otro no, sería 201.
Y el siguiente término de 2, 10, 12, 16, 18, todos los pares que empiezan con «d», también sería 200.
Saludos
Rebeca
Me gustaMe gusta
[…] y geométricas, que son los incrementos que se dan en las sucesiones. Sobre eso escribí aquí y […]
Me gustaMe gusta
[…] y la de la segunda es aritmética (ver más sobre patrones, series, progresiones y sucesiones aquí y aquí). Todas las tablas serían similares, sólo cambia la base y, por tanto, qué tan rápido […]
Me gustaMe gusta
[…] entre otras cosas, la comprensión de patrones (ver más sobre series, patrones y sucesiones aquí y aquí) y relaciones entre cantidades y/o expresiones, el lograr la interpretación relacional del […]
Me gustaMe gusta
[…] límite pasa algo similar a lo que ocurre con los conceptos de sucesión, serie y patrón (ver más aquí y aquí). Son conceptos que permiten interpretaciones que pueden resultar muy diferentes. Es decir, […]
Me gustaMe gusta
[…] cálculos, sólo usando el pensamiento lógico (ver más aquí y aquí) y los patrones (ver más aquí) que se observan al escribir los números en el sistema […]
Me gustaMe gusta
[…] sucesión aritmética de primer orden que empieza en el (1,2), con d=2 (ver más sobre sucesiones aquí y […]
Me gustaMe gusta
[…] la entrada pasada (ver aquí) vimos la diferencia entre sucesión, serie y patrón de formación, conocimos algunas formas de […]
Me gustaMe gusta
¡Fantástico!
En Honduras manejamos los mismos términos Rebeca. Es interesante la conexión entre este estos conceptos y nuestro entorno. La vida está llena de patrones, comportamientos predecibles y otros no tanto claro, pero definitivamente esto es lo que amamos de la matemática, las posibilidades, las estrategias, la creatividad, no terminaría…
Quedé asombrado con lo referente a la desintegración audioactiva, debo confesar que estuve muchas horas tratando de descifrar, quizá me tomaría días estar pensándolo, jeje, pero quería terminar de leer el post.
Hace unos cuantos años (unos 8 creo) me encontré con la sucesión : 2,10,12,16,17,18,19,? … Lo dejo para que los demás lectores digan cuál es el siguiente término…
Además para cada sub-sucesión de la sucesión anterior ¿Cuál término sigue?:
2,12,17,19, … ?
2,10,12,16,18, … ?
En ese entonces entendí que los patrones no son propios a las operaciones aritméticas.
Saludos
Me gustaLe gusta a 1 persona
Muchas gracias por tu comentario, Henry, y por la información sobre el uso de la palabra «serie» en Honduras. Esperemos a ver si alguien de algún otro país tiene alguna otra interpretación local no-matemática para la palabra.
Muy interesantes las sucesiones que propones, son del mismo tipo de la de 1, 11, 21, 1211… conocidas también como «mira y di» (look and say).
Esperemos que los lectores nos digan cuáles son los siguientes términos para cada una.
Saludos
Me gustaLe gusta a 1 persona
Hola Henry ,
El siguiente término de la sucesión de 2,10,12,16,17,18,19,? es 27
Me gustaMe gusta