Elijo lo que voy a escribir basándome en lo que veo importante compartir, según las dificultades que observo en mis hijos y alumnos, y lo que me comentan profesores, papás y lectores del blog. Me he dado cuenta de que las tablas de multiplicar son uno de esos temas que es muy importante compartir.
En la tercera entrada, sobre sentido numérico (ver aquí), comenté por qué es importante ser creativo y flexible al hacer operaciones numéricas, lo cual implica conocer a profundidad las tablas de multiplicar.  En esta entrada y en la de la próxima semana compartiré algunas ideas que pueden servir para que esas elusivas tablas dejen de ser el enemigo y se conviertan en el aliado de los niños (y no tan niños) al enfrentar tareas matemáticas. Para que aquellos que aún no «se saben las tablas», vean una luz al final del túnel, mediante una forma diferente de acercarse a ellas.
En esta entrada y en la de la próxima semana compartiré algunas ideas que pueden servir para que esas elusivas tablas dejen de ser el enemigo y se conviertan en el aliado de los niños (y no tan niños) al enfrentar tareas matemáticas. Para que aquellos que aún no «se saben las tablas», vean una luz al final del túnel, mediante una forma diferente de acercarse a ellas.
¿Qué significa multiplicar?
 La multiplicación es una suma reiterada de un número (multiplicando), la cantidad de veces que indica otro número (multiplicador).
La multiplicación es una suma reiterada de un número (multiplicando), la cantidad de veces que indica otro número (multiplicador).
Por lo tanto, la expresión 5 x 3, en la cual el 5 es el multiplicando y el 3 es el multiplicador, indica que es necesario sumar tres veces el cinco:
5 x 3 = 5 + 5 + 5 = 15
Por extraño que parezca, en otros idiomas la forma correcta de entender la multiplicación puede ser distinta:
5 x 3 en inglés se dice “five times three”, que se traduce como “5 veces 3” y, por lo tanto, 5 x 3 = 3 + 3 + 3 + 3 + 3 = 15. Si bien el resultado es exactamente el mismo que 5 + 5 + 5, éste proceso corresponde a 3 x 5, es decir “three times five”, que se traduce como «3 veces 5».
Entendido así, se considera multiplicador al primer número y multiplicando al segundo.
A ambos elementos (multiplicando y multiplicador) se les denomina factores.
Es bastante conocida la propiedad conmutativa de la multiplicación a través de la expresión “el orden de los factores no altera el producto”. Esto es: 3 x 5 = 5 x 3 = 15, en cualquier idioma. Por tanto, sólo al expresar la multiplicación como suma debe conocerse la interpretación adecuada según el contexto o idioma.
De hecho, si se buscan imágenes de las tablas de multiplicar en Internet, puede observarse que
La “Tabla del 9” normalmente es ésta:
9 x 1 = 9
9 x 2 = 18
9 x 3 = 27…
Mientras que la “9 times table” puede ser ésta:
1 x 9 = 9
2 x 9 = 18
3 x 9 = 27…
Interesante ¿no? Debe tomarse en cuenta cuando tenemos alumnos que transitan de un idioma a otro o de un país a otro.
¿Por qué son difíciles de memorizar?
Considero que el problema no son las tablas en sí, sino los métodos que se usan para que aprenderlas.
 Aprendérselas “recitadas” en orden hace que, cuando se necesite una multiplicación por un número grande, se requiera pasar por todas las multiplicaciones anteriores: 7 x 1 = 7… 7 x 2 = 14… 7 x 8 = 56… Supongo que yo también las aprendí recitando, incluso me recuerdo a mí misma recitándolas en reversa y equivocándome en 8 x 4… frente a todo el grupo. Ahora considero que ése es un método poco eficiente. Conozco jóvenes que necesitan escribir todas las tablas en un lado del examen para tenerlas a la mano cuando las necesiten. Eso les quita mucho tiempo valioso para atender los problemas que les están planteando y que muy probablemente sí saben resolver, sólo que no los alcanzan a hacer dado lo que se tardan en hacer las operaciones.
Aprendérselas “recitadas” en orden hace que, cuando se necesite una multiplicación por un número grande, se requiera pasar por todas las multiplicaciones anteriores: 7 x 1 = 7… 7 x 2 = 14… 7 x 8 = 56… Supongo que yo también las aprendí recitando, incluso me recuerdo a mí misma recitándolas en reversa y equivocándome en 8 x 4… frente a todo el grupo. Ahora considero que ése es un método poco eficiente. Conozco jóvenes que necesitan escribir todas las tablas en un lado del examen para tenerlas a la mano cuando las necesiten. Eso les quita mucho tiempo valioso para atender los problemas que les están planteando y que muy probablemente sí saben resolver, sólo que no los alcanzan a hacer dado lo que se tardan en hacer las operaciones.
 Aprendérselas “cantando” es, creo, aún menos útil, porque con ciertos ritmos se canta más lento de lo que se recita, al llevar en la mente el ritmo además de la “letra”. Además de que los papás y hermanos pueden llegar a desesperarse por las canciones mucho antes de que el niño se aprenda las dichosas tablas… ¿O no?
Aprendérselas “cantando” es, creo, aún menos útil, porque con ciertos ritmos se canta más lento de lo que se recita, al llevar en la mente el ritmo además de la “letra”. Además de que los papás y hermanos pueden llegar a desesperarse por las canciones mucho antes de que el niño se aprenda las dichosas tablas… ¿O no?
 Habrán notado que lo que se memoriza sin ninguna conexión con algo más, queda muy débil en la memoria y se olvida fácilmente. Recitar o cantar le da solo un poco de conexión a las multiplicaciones. Si bien hace que las aprendamos por bloques de información, esto pronto deja de ser útil. Mientras en la escuela sólo estamos contestando ejercicios de multiplicación, puede ser suficiente sabernos las tablas por bloques y en orden. Cuando empezamos a dividir, sacar raíces cuadradas, factorizar… necesitamos tener los conocimientos almacenados en la memoria de una mejor manera.
Habrán notado que lo que se memoriza sin ninguna conexión con algo más, queda muy débil en la memoria y se olvida fácilmente. Recitar o cantar le da solo un poco de conexión a las multiplicaciones. Si bien hace que las aprendamos por bloques de información, esto pronto deja de ser útil. Mientras en la escuela sólo estamos contestando ejercicios de multiplicación, puede ser suficiente sabernos las tablas por bloques y en orden. Cuando empezamos a dividir, sacar raíces cuadradas, factorizar… necesitamos tener los conocimientos almacenados en la memoria de una mejor manera.
Existen diversas estrategias que permiten un mejor aprendizaje, práctica y uso de las tablas, por lo que dedicaré no una, sino dos entradas a presentar y explicar esas estrategias, para que puedan elegir aquellas que mejor les funcionen según el estilo de quien las va a aprender. Comencemos.
Patrones dentro de las tablas de multiplicar
 Una de las bases de las matemáticas es el reconocimiento de patrones. Considero que, si presentamos a los alumnos las tablas acomodando las operaciones y resultados de forma que se vean claramente los patrones que siguen (usando colores, por ejemplo), lograremos que tengan más sentido para él, que puedan entenderlas mejor y, con ello, las aprendan y las use más fácilmente.
Una de las bases de las matemáticas es el reconocimiento de patrones. Considero que, si presentamos a los alumnos las tablas acomodando las operaciones y resultados de forma que se vean claramente los patrones que siguen (usando colores, por ejemplo), lograremos que tengan más sentido para él, que puedan entenderlas mejor y, con ello, las aprendan y las use más fácilmente.
En vez de darle una lista de operaciones a memorizar, le damos una imagen a analizar para que encuentre los patrones y las relaciones dentro de ella y esos patrones, junto con otras actividades complementarias, le ayuden a ir memorizando los resultados de forma más eficiente.
Lo anterior también ayuda a reconocer la divisibilidad de los números, la cual será necesaria, entre otras cosas, para simplificar fracciones (ver más aquí).
Además, si escribimos cada operación con los dos órdenes, el alumno se acostumbrará a la propiedad conmutativa de la multiplicación y se aprenderá dos multiplicaciones a la vez, lo cual es un buen ahorro de tiempo.
Tabla del cero
Puede parecer innecesaria, pero conviene que desde pequeños los niños se vayan acostumbrando a que el cero es el elemento absorbente de la multiplicación. Esto es, al multiplicar cualquier número por cero siempre se obtiene cero. En este caso, más que aprenderse una tabla, comprenden un concepto matemático y lo aplican, lo cual es mucho más útil que la simple memorización.
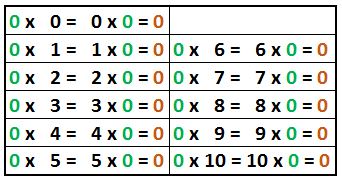
Tabla del uno
También puede parecer innecesaria, pero también conviene que los niños se acostumbren a que el uno es el elemento neutro de la multiplicación. Esto es, al multiplicar cualquier número por uno se obtiene el número original.

Otras características especiales del cero y el uno pueden verse aquí.
Tabla del dos
Con la tabla del dos ya comienza a haber algo de “acción”. Recordando lo que significa multiplicar, podemos observar que:
2 x 4 = 2 + 2 + 2 + 2 = 8 = 4 x 2 = 4 + 4
Por lo tanto, los resultados de la tabla del dos de pueden obtener duplicando el segundo número (sumándolo a sí mismo). Además, todos los resultados de la tabla del dos son pares y las unidades se repiten en esta secuencia: 0, 2, 4, 6, 8, 0…

Tabla del tres
Algo similar se puede hacer con la tabla del tres:
3 x 4 = 3 + 3 + 3 + 3 = 12 = 4 x 3 = 4 + 4 + 4
Esto es, los resultados de la tabla del tres de pueden obtener triplicando el segundo número (sumándolo a sí mismo tres veces).
Podemos notar este interesante patrón en la tabla del tres: por su característica de avanzar de 3 en 3, para las multiplicaciones del 1 al 9, las unidades avanzan del 1 al 9 de izquierda a derecha de arriba hacia abajo y en la segunda y tercera columnas las decenas son 1 y 2 respectivamente.
Además, para esas mismas multiplicaciones (3 por 1 al 9) si sumamos los dígitos de los números del primer renglón, obtenemos 3, en los del segundo, obtenemos 6 y en los del tercero, obtenemos 9. Todas las sumas de los dígitos son múltiplos de 3 y eso ocurre con todos los números que resultan de una multiplicación por 3. Podemos ver que van intercalados: uno impar, uno par.
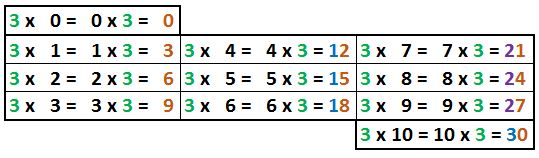
Tabla del cuatro
Para la del cuatro podemos recordar que al multiplicar por cuatro obtenemos el doble que al multiplicar por dos. También podemos observar este interesante patrón: si la decena es par, la unidad es 0, 4 u 8. Si la decena es non, la unidad es 2 o 6. Eso ocurre con todos los números que son resultado de multiplicar por 4. Como en la tabla del dos, las unidades también se repiten en secuencia: 0, 4, 8, 2, 6, 0…

En general, las primeras tablas son sencillas de aprender porque son números pequeños y pueden hacerse los cálculos rápidamente al principio y, posteriormente, memorizar los resultados.
Tabla del cinco
La tabla del cinco sigue un patrón muy interesantes que pueden servirnos para relacionar los resultados: Al multiplicar por 5 obtenemos el mismo resultado que al multiplicar por 10 y dividir entre 2, por lo que
Todas las multiplicaciones de 5 por un número par tienen la mitad de ese número par en la decena y un 0 en la unidad:
5 x 6 = 10 x 6 / 2 = 30. (3 es la mitad de 6)
Todas las multiplicaciones de 5 por un número impar terminan en 5 y la decena es la mitad del número anterior:
5 x 7 = 10 x 7 / 2 = 35 (3 es la mitad de 6, el número anterior a 7).

Tabla del seis
Con la del seis podemos pensar en el doble de la del tres o en el triple de la del dos. Es decir, si sabemos que 3 x 7 = 21, entonces 6 x 7 = 42. O si recordamos que 2 x 6 = 12, entonces 6 x 6 = 36… y así.
Como en las tablas del dos y cuatro, todos los resultados son pares y las unidades se repiten en secuencia, en este caso: 0, 6, 2, 8, 4, 0…
Con los números pares de la tabla del seis hay otro patrón: como el 6 es el número que sigue del 5, entonces al multiplicar un 6 por un par la decena es la mitad del número y la unidad es el número:
6 x 2 = 12, (1 es la mitad de 2) 6 x 8 = 48, (4 es la mitad de 8)…

Tabla del siete
El siete es un número que, por ser el complemento para diez del tres, también tiene un patrón interesante en su tabla, del 1 al 9. La unidad de cada siguiente resultado es más chica en tres unidades que la anterior, por eso se puede observar este patrón en los resultados: Las unidades van del 1 al 9 de izquierda a derecha de abajo a arriba. Las decenas no tienen un patrón tan claro: empieza con el 0, luego el 1, el 2 que se repite, luego el 3 y después el 4, que también se repite, luego el 5 y el 6. El 2 y el 4 se repiten y los demás no.

Tabla del ocho
Para la tabla del ocho se puede hacer algo similar que para la del cuatro con el dos: duplicar los resultados de la del cuatro. Además, al estar viendo siempre las multiplicaciones en los dos órdenes, a esta altura ya sabemos multiplicar 8 por casi todos los números, sólo nos falta por 8 y por 9.

Como en las tablas del 2, 4 y 6, los números son pares y las unidades se repiten en secuencia, en este caso: 0, 8, 6, 4, 2, 0… Con el 2 la secuencia es ascendente, con el 8 es descendente (por ser el complemento a diez de dos) y en el 4 y 6 van intercalados de forma invertida, por ser ambos complementos a diez entre sí.
Tabla del nueve
Dediqué una entrada completa a las interesantes características del nueve, incluyendo la forma de multiplicar usando las manos (ver aquí). El patrón que se puede observar en la tabla escrita, a partir de 9 x 1 es que las unidades van descendiendo y las decenas van ascendiendo de forma tal que la suma de ambas siempre sea 9.

Tabla del diez
Para la del diez sólo hay que recordar que multiplicar un entero por 10 equivale a agregar un 0 a la derecha (ver más aquí). No necesita enseñarse en orden, se enseña más bien la regla (y por qué funciona) y se les puede preguntar cualquier multiplicación por diez en cualquier orden y podrán obtenerla fácilmente.
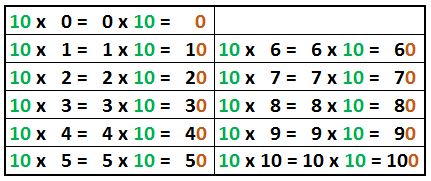
Veamos ahora un par de ideas más para practicar las tablas de multiplicar.
Tarjetas con multiplicaciones
Se necesitan tarjetas de cartulina. Para cada multiplicación, hacer dos tarjetas, una por cada orden, aunque aún no se haya practicado la otra tabla. Es decir, si se están practicando las tablas hasta la del tres, se hacen todas las tarjetas de las tablas del 0, 1, 2 y 3 en ambos órdenes, teniendo tanto la tarjeta de 3 x 10 como la de 10 x 3.
Se llenan por un lado con la pregunta sin respuesta: 3 x 10 =
Se llenan por el otro lado con la pregunta con respuesta: 3 x 10 = 30
Aquí está un ejemplo de las dos tarjetas con la multiplicación que suele ser la menos sencilla de aprender, y que encabeza esta entrada:
7 x 8 = 8 x 7 = 56

Una vez revisados los patrones de cada tabla que presenté y que estemos familiarizados con los resultados, se mezclan las tarjetas, todas con la cara sin respuesta para el mismo lado, y se empiezan a pasar una a una para revisar si nos la sabemos. Se acomoda cada tarjeta en uno de tres montones: uno tiene las multiplicaciones que nos sabemos muy bien, otro las que nos cuestan un poco de trabajo y otro las que no nos sabemos o nos cuestan mucho trabajo.
 Lo normal es que el montón de las que nos sabemos muy bien sea más alto que los otros (porque ahí estarán todas las multiplicaciones por uno, por cero y por diez, que son muy fáciles de recordar). Eso levanta mucho el ánimo de quien está practicando. Una vez que notamos que nos faltan pocas por aprender, podemos practicar sólo con esas tarjetas, buscando formas de memorizar los resultados con base en los patrones presentados o en algún otro truco mnemotécnico. Tener la respuesta atrás de la tarjeta ayuda a que podamos comprobarla rápidamente.
Lo normal es que el montón de las que nos sabemos muy bien sea más alto que los otros (porque ahí estarán todas las multiplicaciones por uno, por cero y por diez, que son muy fáciles de recordar). Eso levanta mucho el ánimo de quien está practicando. Una vez que notamos que nos faltan pocas por aprender, podemos practicar sólo con esas tarjetas, buscando formas de memorizar los resultados con base en los patrones presentados o en algún otro truco mnemotécnico. Tener la respuesta atrás de la tarjeta ayuda a que podamos comprobarla rápidamente.
Después se mezclan todas tarjetas y se repite el proceso hasta que todas las tarjetas queden en el montón de las que nos sabemos muy bien.
Se van incrementando las tarjetas correspondientes conforme nos vamos aprendiendo nuevas tablas. Ojo: algunas ya estarán, dado que, por ejemplo, al integrar la tabla del cuatro ya se tedrán 4 x 0, 4 x 1, 4 x 2 y 4 x 3.
Para cuando llegamos a la tabla del siete, sólo se requiere agregar las tarjetas de 7 x 7, 7 x 8, 8 x 7, 7 x 9, 9 x 7, 7 x 10, 10 x 7. ¡Sólo 7 tarjetas por aprender! Para la del ocho sólo faltarán 5 tarjetas, para la del nueve sólo 3 y para la del 10 sólo 1. Eso anima mucho, ¿no creen?
Multiplicar en vez de contar uno por uno
 Encontrarle utilidad a lo que aprendemos ayuda a que sea menos pesado aprenderlo y a que lo recordemos más fácilmente. Una estrategia que va en ese sentido es aprovechar las multiplicaciones para contar rápidamente algo que esté ordenado en forma rectangular, como estas galletas. En vez de contar una por una, podemos contar cuántas filas (10) y cuantas columnas (6) hay, hacer la multiplicación: 10 x 6 = 60, y llegar al resultado rápidamente: 60 galletas.
Encontrarle utilidad a lo que aprendemos ayuda a que sea menos pesado aprenderlo y a que lo recordemos más fácilmente. Una estrategia que va en ese sentido es aprovechar las multiplicaciones para contar rápidamente algo que esté ordenado en forma rectangular, como estas galletas. En vez de contar una por una, podemos contar cuántas filas (10) y cuantas columnas (6) hay, hacer la multiplicación: 10 x 6 = 60, y llegar al resultado rápidamente: 60 galletas.
Para cerrar
 «Saberse las tablas» es indispensable para que el tiempo asignado alcance para realizar actividades matemáticas, como multiplicar números grandes, dividir, sacar raíces cuadradas, factorizar y todas aquellas actividades que incluyan a éstas. Puede enfrentarse el reto de aprenderlas desde perspectivas distintas, según el estilo de cada persona. Si aprovechamos que las tablas muestran patrones en sus resultados, además de facilitarnos su aprendizaje, estaremos desarrollando a la par el sentido numérico y el pensamiento lógico (ver más aquí).
«Saberse las tablas» es indispensable para que el tiempo asignado alcance para realizar actividades matemáticas, como multiplicar números grandes, dividir, sacar raíces cuadradas, factorizar y todas aquellas actividades que incluyan a éstas. Puede enfrentarse el reto de aprenderlas desde perspectivas distintas, según el estilo de cada persona. Si aprovechamos que las tablas muestran patrones en sus resultados, además de facilitarnos su aprendizaje, estaremos desarrollando a la par el sentido numérico y el pensamiento lógico (ver más aquí).
Los espero la próxima semana con más ideas para facilitar el dominio de las tablas de multiplicar y su empleo en otros contextos.
Como siempre, gracias por leer y compartir. Pueden escribirme si quedó alguna duda, si quieren hacer algún comentario sobre su experiencia con estas estrategias o si quieren sugerir algún tema para una entrada posterior en este blog.
Rebeca
PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.
PD2: Quiero agradecer a estas dos páginas en las que me apoyo constantemente para redactar el blog: https://pixabay.com/ http://webresizer.com/ y a Excel y Word, en los que elaboré las tablas y el dibujo principal.



[…] par siempre da un número terminado en cero (ver lo que he escrito sobre las tablas de multiplicar aquí y […]
Me gustaMe gusta
[…] cierto, ha publicado algunas propuestas sobre cómo trabajar con las tablas de multiplicar aquí y […]
Me gustaMe gusta
[…] muchos no se sepan las tablas de multiplicar completas tampoco ayuda (ver ideas para trabajarlas aquí, aquí y […]
Me gustaMe gusta
Muchas gracias por la entrada, Rebeca!
Me gustaMe gusta
🙂
Me gustaMe gusta
[…] encontrar más formas de practicar las tablas en estas dos entradas de este blog (uno y […]
Me gustaMe gusta
[…] además es importante saberse las tablas de multiplicar, sobre ellas escribí las entradas 14 y […]
Me gustaMe gusta
[…] como base para lograr el nuevo aprendizaje (ver ideas para aprender las tablas de multiplicar aquí y […]
Me gustaMe gusta
[…] Las tablas de multiplicar: ¿cómo transformarlas en nuestras aliadas? (ver aquí) […]
Me gustaMe gusta
[…] Las tablas de multiplicar: ¿cómo transformarlas en nuestras aliadas? (ver aquí) […]
Me gustaMe gusta
[…] nos sabemos o podemos calcular fácilmente las tablas del 1 al 10 (ver estrategias para aprenderlas aquí y aquí), la división entre un número del 1 al 10 es razonablemente […]
Me gustaMe gusta
[…] distinta. Pueden leer más al respecto en la primera entrada sobre las tablas de multiplicar (ver aquí). La segunda entrada sobre las tablas de multiplicar (ver aquí) contiene más estrategias y formas […]
Me gustaMe gusta
[…] lo tanto, 7 x 8 = 8 x 7 = 56 (ver más ideas para comprender y memorizar las tablas de multiplicar aquí y […]
Me gustaMe gusta
[…] de hasta 2 cifras y sólo 19 de los 100 posibles serán cero (ver más sobre tablas de multiplicar aquí y […]
Me gustaMe gusta
[…] hacer cálculos lo más rápido que pueden (ver ideas para aprenderse las tablas de multiplicar aquí y aquí). Para ellos se escriben libros como Método Simplificado de Multiplicación y Cálculo […]
Me gustaMe gusta
[…] usar para enseñar diversos conceptos y procedimientos, como las tablas de multiplicar (ver más aquí y […]
Me gustaMe gusta
[…] llegar al final. Ver más sobre las tablas de multiplicar, para tomar ideas sobre cómo preguntar, aquí y […]
Me gustaMe gusta
[…] la primera entrada sobre tablas de multiplicar (ver aquí) mencioné que, según el idioma y país, el concepto de multiplicación se entiende distinto y la […]
Me gustaMe gusta
[…] escribí sobre las tablas de multiplicar (ver aquí), también observamos patrones en su […]
Me gustaMe gusta
Rebe: muchas gracias por darnos estas herramientas de aprendizaje tan útiles!!! Si bien estamos acostumbrados a memorizar sin entender es fundamental explicarles a los niños el porque de los resultados y de una manera visual mucho muy clara para poder ayudar a que se queden en la memoria.
Me gustaLe gusta a 1 persona
De nada, Marifer, muchas gracias a ti por tu comentario.
Sí, para las personas más visuales, el acomodar las cosas de cierta forma y marcar los patrones con colores puede resultar muy útil. Y, para todos, el entender los “porqué” ayuda mucho a que se dé el aprendizaje, y dure. Espero que estas ideas les funcionen muy bien a tus niños.
¡Saludos!
Me gustaMe gusta
[…] la entrada anterior (ver aquí) presenté tres estrategias para aprender y practicar las tablas de multiplicar. Una basada en […]
Me gustaMe gusta
Me encantó esta entrada! estoy segura que cuando vea este tema con mis alumnitos y aplique la estrategia, les irá súper bien con las tablas!! Gracias Rebeca!
Me gustaLe gusta a 1 persona
Muchas gracias por tu comentario, Ericka! Confío en que les irá muy bien con las tablas a tus alumnos con estas estrategias (y las de la próxima semana) y, sobre todo, con tu entusiasmo para acompañarlos en su aprendizaje.
Saludos!
Me gustaMe gusta