En la segunda entrada de este blog (ver aquí) mencioné que considero el pensamiento lógico-matemático el primer pilar de una buena relación con las matemáticas. En una entrada posterior (la 18, ver aquí) escribí más sobre su utilidad y compartí algunas ideas para fomentarlo.
Hoy les presento una nueva idea para desarrollar el pensamiento lógico matemático: crear y usar material lógicamente estructurado. Al hablar de este material normalmente se hace referencia a algo físico, manipulable, pero propondré también hoy unas opciones “abstractas” para apoyar el aprendizaje eficiente (ver más aquí), en este caso, desarrollar ese pensamiento mientras se aprende algún otro tema de matemáticas. Leer más »
En la entrada anterior (ver 
He comentado en ocasiones anteriores que las matemáticas son la ciencia del reconocimiento de patrones. También puede considerarse que es una ciencia que nos permite tanto entender el orden de lo que observamos, como explicarlo, mediante cadenas de razonamientos, a través de objetos matemáticos.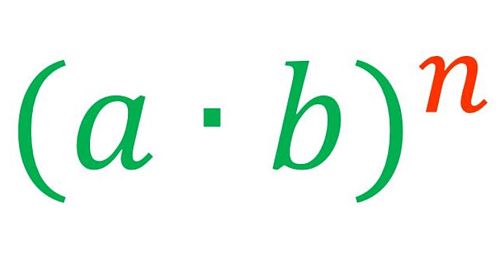
Conociendo los cuidados que se deben tener según la estructura de la expresión (ver más sobre sentido de estructura
Como en toda la matemática, conviene que los profesores de cualquier grado escolar tengan una idea acerca de los temas futuros en los que se va a usar lo que están enseñando actualmente a sus alumnos. Así podrán, tanto sembrar buenas semillas en ellos, como evitar los atajos que puedan provocarles problemas más adelante. Por ello, esta entrada parte de lo aritmético y llega a lo algebraico.
Había escrito previamente una entrada sobre cómo hacer preguntas con intención didáctica clara, que va en este mismo sentido (ver 
Listo, después de aprender sobre el tema la semana anterior, nos hemos vuelto hábiles con las reglas de tres directas e inversas. Ahora nos proponen un problema que parece como de regla de tres, pero no tiene tres, sino ¡cinco! datos. ¿Qué hacemos?
Estamos ante un problema escrito y descubrimos que contamos con tres datos numéricos y un cuarto dato desconocido, que es lo que nos preguntan. ¿Eso por si sólo convierte al problema en uno de regla de tres? No necesariamente, los problemas que pueden resolverse con una regla de tres tienen características especiales. Además, hay de diferentes tipos y cada uno tiene su propia forma de resolverse.
Estoy 100% segura de que hay mucho que se puede decir sobre los porcentajes. ¿Qué significan? ¿Para qué se usan? ¿Cómo se calculan? ¿Qué cuidados debemos tener con ellos?, entre otras.
IMPULSO MATEMÁTICO 