Esta entrada va dedicada a Salvador, en recuerdo de esas interminables horas estudiando juntos, tanto matemáticas como otras materias, a lo largo de la preparatoria y la carrera de ingeniería industrial.
Ahora explico por qué: buscando alguna idea sobre qué escribir para esta entrada, ¡la número 23 ya! recordé que, durante un torneo de futbol en la universidad, Salvador mencionó que había elegido como número de su uniforme el 23 porque jugaba dos – tres (en México eso significa poco mejor que regular). Así como él lo hizo en ese momento, hay muchas formas de reinterpretar los números, de jugar con ellos, y todas ellas nos permiten desarrollar el sentido numérico, que yo considero el segundo pilar en la buena relación con las matemáticas (ver la primera entrada al respecto aquí).
Para mí el primer pilar es el pensamiento lógico matemático, del que ya he escrito dos entradas (ver aquí y aquí). Ésta será la segunda dedicada específicamente al sentido numérico. También encontrarán referencias a alguno de los dos pilares, o a ambos, en muchas de las otras entradas que he escrito. Por cierto, incluiré un breve apartado sobre jerarquía de las operaciones matemáticas, para que tengamos a la mano las reglas con las que se rigen los juegos con los números.
Creo sinceramente que, desarrollando esos dos pilares y entendiendo bien los porqués de los conceptos y procesos matemáticos, todos podemos llevar una muy buena relación con las matemáticas. Para apoyar en ese sentido escribo este blog.Leer más »
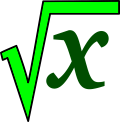Esta entrada me la sugirió Marifer Calva hace unas semanas (gracias por ello, Marifer). La idea central es comprender el proceso de la extracción de la raíz cuadrada de un número, sólo que para ello conviene comprender antes qué es un número irracional. Veremos también cómo usar los patrones que observamos, en los cuadrados de los primeros 10 números, para deducir raíces cuadradas exactas de números hasta 10 000.
Escribiré, en esta entrada y en la siguiente, tanto sobre las sucesiones y series más sencillas, como sobre algunas más complejas, para que todos los profesores y papás con hijos en distintos niveles escolares encuentren algo útil y, lo más importante, entiendan de dónde viene y hacia dónde va este tema. Recuerden la importancia de las conexiones entre conocimientos.
Los profesores y los papás hacemos preguntas a nuestros alumnos e hijos y esperamos provocar en ellos un proceso de pensamiento (como fichas de dominó que caen una tras otra, o como algo más complejo) que los lleven a ciertas respuestas. Para algunas preguntas, las respuestas pueden obtenerse y/o expresarse de diferentes formas. Según la intención didáctica de la pregunta (lo que queremos que aprendan al contestarla), puede ser necesario que sea respondida de cierta forma y/o con cierto proceso. Sobre eso compartiré algunas ideas hoy.
Hoy compartiré algunas ideas que pueden ayudar a desarrollar el pensamiento lógico matemático en personas de todas las edades. Expliqué en la segunda entrada del blog (ver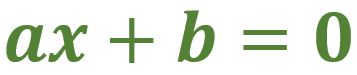 
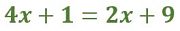Ahora escribiré sobre lo que es una ecuación, lo que significa “resolver una ecuación” y los cuidados que son necesarios al “resolver una ecuación lineal con una incógnita”. También incluiré una sugerencia sobre cómo plantear ejercicios en primaria que preparen a los alumnos para resolver ecuaciones lineales en secundaria.
En la entrada anterior (ver 
En esta entrada y en la de la próxima semana compartiré algunas ideas que pueden servir para que esas elusivas tablas dejen de ser el enemigo y se conviertan en el aliado de los niños (y no tan niños) al enfrentar tareas matemáticas. Para que aquellos que aún no «se saben las tablas», vean una luz al final del túnel, mediante una forma diferente de acercarse a ellas. 
IMPULSO MATEMÁTICO 