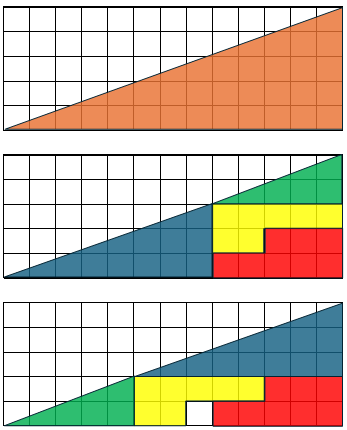
Esta es la entrada 404 de este blog. Voy a aprovechar para contarles la experiencia con una actividad de aprendizaje basada en la imagen que encabeza esta entrada. Viene bien que sea la 404. En el mundo de la informática el Error 404 indica que hay algo que no se encontró y, si uno revisa a ojo las cuatro piezas que se reacomodan entre la imagen de en medio y la de abajo, no encuentra cómo es que en la imagen de abajo hay un cuadrito que ya no alcanzó color.
Les entregué a las niñas a las que apoyo una hoja por cada dos niñas, un lápiz y una regla y les pedí que revisaran las tres imágenes y me explicaran cómo es que las tres ocupaban el mismo espacio si en la de abajo había un cuadrito extra que no tenía color.
Fue más de media hora de analizar por aquí y por allá las tres imágenes. Fue necesario explicarles el concepto de área como el número de cuadritos sombreados, la fórmula del área de un triángulo y algunas cosas más. Contaban, medían, pensaban que habían entendido y al explicarlo veían que no, pero en el camino aprendían/recordaban conceptos importantes.
¡Un montón de neuronas en movimiento! Fue maravilloso.
Lo malo es que se nos acabó el tiempo disponible, caray, así que fue necesario orientarlas para que usaran la regla para ver que las inclinaciones de los dos triángulos no eran las mismas y, por tanto, la imagen de en medio está un poco «panda», «curveada hacia abajo» y su área es solo 32 u^2, mientras que la imagen de abajo está un poco «curveada hacia arriba» y su área es 33 u^2. El triángulo de arriba, el que tiene una diagonal que sí es una recta, tiene un área de 33.5 u^2, a medio camino entre los otros dos.
Una linda ilusión óptica que se descubre usando matemáticas.
Así cerramos la actividad, explicando que a veces la primera impresión, o la vista y otro sentido nos «dan» una cosa que no es real. Y muchas veces usando matemáticas podemos descubrir el truco.
Confío en poco a poco irlas convenciendo de las grandes ventajas de saber matemáticas para desenmascarar trucos de magia / engaños reales.
¡Hasta el próximo miércoles!
PD: Quiero agradecer a esta página en la que me apoyo constantemente para redactar el blog: pixabay.
Cuando pensamos en “medir” algo, desde el punto de vista geométrico, suele venir a la mente el medir el largo, o el largo y ancho, o largo, ancho y alto, incluso el perímetro. Sin embargo, hay al menos otra medición que es importante en geometría: el ángulo de abertura entre dos rectas, si pensamos en dos dimensiones solamente. Es por eso que los “juegos de geometría”, como les llamamos en México, incluyen, además de la regla graduada y las escuadras, el transportador, que usamos, justamente, para medir ángulos.
IMPULSO MATEMÁTICO 