Ésta es la entrada 62 de este blog. La dedicaremos a las conversiones de las unidades de medida básicas (longitud, área, volumen y masa) en el Sistema Internacional de Unidades. En una entrada posterior complementaremos con conversiones de otras unidades dentro de ese mismo sistema y con conversiones dentro, hacia y desde el Sistema Inglés de Unidades.

¿Qué es una magnitud?

Según el diccionario de la Real Academia de la Lengua Española, magnitud, en física, es una propiedad física (valga la redundancia) que puede ser medida.

Las primeras magnitudes que conocemos son la longitud, el área, el volumen y la masa. Las vemos en la materia de Matemáticas en la educación primaria, quizá con algunas aplicaciones en Ciencias Naturales. Existen muchas magnitudes más que vamos conociendo conforme avanzamos en la escuela, incluso en otras materias, como la luminosidad, la temperatura, etcétera.

El tiempo es una magnitud que se usa frecuentemente en física, aunque no sea una propiedad física de un objeto dado, más bien es una propiedad de una situación o movimiento dado, como todas las magnitudes relacionadas con el tiempo (velocidad, aceleración, etcétera). Ver más sobre el reloj y los cálculos con el tiempo aquí.

¿Para qué sirven las magnitudes?

Reconocer y medir las magnitudes o propiedades de los objetos es necesario para poder comparar ese objeto con otro o con una situación en particular. Podemos identificar cuál objeto tiene más masa que otro, cuál mide lo suficiente como para cubrir un requisito, incluso podemos comparar algo consigo mismo, si la propiedad que estamos midiendo va cambiando en el tiempo, como la estatura de una niña al crecer.

De hecho, al medir alguna propiedad, la comparamos contra una unidad de medida base. Veamos algunas de ellas.

Sistema Internacional de Unidades

El Sistema Internacional de Unidades se basa en siete unidades de base correspondientes a las magnitudes de longitud (metro), masa (kilogramo), tiempo (segundo), corriente eléctrica (ampere), temperatura (kelvin), cantidad de materia (mol), e intensidad luminosa (candela). A partir de éstas se determinan todas las demás. Si tienen curiosidad de saber cómo se define cada de las unidades de base, vean la información después del cierre de esta entrada.

Unidades de longitud en el Sistema Internacional de Unidades

La unidad de longitud base es el metro. Si vamos a medir distancias muy grandes, como de una ciudad a otra, necesitamos una referencia más grande. Si vamos a medir distancias muy pequeñas, como el tamaño de un lápiz, necesitamos una referencia más pequeña.

Para eso existen los múltiplos y submúltiplos de la unidad base, que se forman y equivalen de esta manera:

1 kilómetro (km) = 1000 metros           1 m = 0.001 km
1 hectómetro (hm) = 100 metros          1 m = 0.01 hm
1 decámetro (dam) = 10 metros           1 m = 0.1 dam
1 metro (m) = 1 metro                             1 m = 1 m
1 decímetro (dm) = 0.1 metros             1 m = 10 dm
1 centímetro (cm) = 0.01 metros          1 m = 100 cm
1 milímetro (mm) = 0.001 metros        1 m = 1000 mm

Conversiones de unidades de longitud en el Sistema Internacional de Unidades

Existen varias formas de entender y hacer las conversiones. Explicaré tres diferentes aquí que, como verán, realmente son sólo distintos enfoques del mismo cálculo:

Como regla de tres directa

Si queremos convertir 35 cm a m

Preparamos las dos columnas y elegimos la equivalencia que nos permita multiplicar:

cm      m
1         0.01
35       ?

? = 35 x 0.01 / 1 = 0.35   ->   35 cm = 0.35 m

(ver más sobre regla de tres aquí):

Pueden ver que si hubieran elegido la otra equivalencia llegan a la misma respuesta:

cm      m
100      1
35        ?

? = 35 x 1 / 100 = 0.35 -> 35 cm = 0.35 m

Como en este caso se multiplica por o divide entre potencias de 10, lo cual equivale a mover el punto decimal hacia derecha o izquierda respectivamente, tantas posiciones como ceros tenga el factor o divisor, realmente es igual de sencillo cualquiera de los dos procesos (ver más sobre el sistema numérico decimal aquí)

Multiplicando por la unidad:

Esta forma de entender la conversión es muy útil, sobre todo cuando se necesita hacer conversiones complejas. Veamos una sencilla y, como siempre en este blog, su justificación:

Nuevamente vamos a convertir 35 cm a m

Escribo los 35 cm y luego los multiplico por un 1 muy especial. Recuerden que el 1 es el elemento neutro de la multiplicación y, por tanto, al multiplicar por 1 el valor permanece (ver más sobre las características del número 1 aquí). Ese 1 está formado por la equivalencia que más nos convenga usar. En este caso, la de 1 cm = 0.01 m. Como ambos lados de la igualdad valen lo mismo, si divido un lado entre el otro obtengo un 1. Elijo la unidad a la que quiero llegar para el numerador y la unidad de la que parto para el denominador.

Ahora hago la operación y “simplifico” las unidades que sean iguales en numerador y denominador, de esta forma:

Listo, llegamos a la misma respuesta por un camino que, en esencia, es el mismo.

Multiplicando/dividiendo por las potencias de 10 que permitan llegar de la unidad de medida inicial a la final

Aquí suele dibujarse una escalera como ésta e indicar que cambiar de una unidad a otra implica cambiar de escalón. Si se va de un escalón superior a uno inferior, se multiplica por 10, una vez por cada escalón. Si se va de un escalón inferior a uno superior, se divide entre 10, una vez por cada escalón, de esta manera:

Por lo tanto, para convertir 35 cm a metros se necesita ir del “escalón” cm al “escalón” m, son 2 escalones, por lo tanto se divide entre 10 dos veces, que equivale a mover el punto decimal 2 posiciones hacia la izquierda.

35 cm = 0.35 m

Esta es la idea básica a partir de la cual se pueden hacer todas las conversiones entre este tipo de unidades de medida. Un cuidado especial que es necesario tener es completar con ceros cuando sea necesario y tener cuidado al proceder cuando se tenga un punto decimal en el dato inicial.

Por ejemplo:

Para convertir 35 cm a km, son 5 escalones hacia arriba, se mueve el punto decimal 5 posiciones hacia la izquierda y se completa con ceros:

35 cm = 0.00035 km

Para convertir 3.5 hm a dm, son 3 escalones hacia abajo, se mueve el punto decimal 3 posiciones hacia la derecha y se completa con ceros:

3.5 hm = 3500 dm

Las dos primeras formas de convertir (por regla de 3 y multiplicando por la unidad) sirven para cualquier conversión y se obtiene la respuesta en un solo paso, si se tiene la equivalencia necesaria. En caso de que no, se usan dos o más pasos para hacer la conversión:

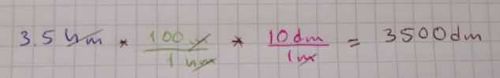
En casos como éste, puede ser más rápido usar el procedimiento de la “escalera”.

Siempre conviene que nuestros hijos y alumnos conozcan más de un camino para resolver lo que se les pida.

Unidades de área en el Sistema Internacional de Unidades:

Las unidades de área son los cuadrados de las unidades de longitud, por lo que las conversiones entre múltiplos y submúltiplos van de 100 en 100, en vez de 10 en 10.

Para entenderlo vean esta comparación de imágenes:

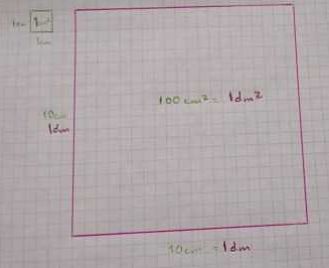
Veamos cómo funcionaría todo lo anterior con medidas de área:

1 kilómetro cuadrado (km²) = 1000000 metros cuadrados      1 m² = 0.000001 km²
1 hectómetro cuadrado (hm²) = 10000 metros cuadrados       1 m² = 0.0001 hm²
1 decámetro cuadrado (dam²) = 100 metros cuadrado            1 m² = 0.01 dam²
1 metro cuadrado (m²) = 1 metro cuadrado                                1 m² = 1 m²
1 decímetro cuadrado (dm²) = 0.01 metros cuadrado              1 m² = 100 dm²
1 centímetro cuadrado (cm²) = 0.0001 metros cuadrado         1 m² = 10000 cm²
1 milímetro cuadrado (mm²) = 0.000001 metros cuadrado     1 m² = 1000000 mm²

Conversiones de unidades de área en el Sistema Internacional de Unidades:

Como regla de tres directa

Si queremos convertir 35 cm² a m²

Preparamos las dos columnas y elegimos (si la tenemos) la equivalencia que nos permita multiplicar:

cm²      m²
1           0.0001
35         ?

? = 35 x 0.0001 / 1 = 0.0035 -> 35 cm² = 0.0035 m²

Pueden ver que si hubieran elegido la otra equivalencia llegan a la misma respuesta:

cm²         m²
10000      1
35            ?

? = 35 x 1 / 10000 = 0.0035 -> 35 cm² = 0.0035 m²

Multiplicando por la unidad

Convertir 35 cm² a m²

Escribo los 35 cm² y luego los multiplico por el 1 formado por la equivalencia de 1 cm² = 0.0001 m²:

Elijo la unidad a la que quiero llegar para el numerador y la unidad de la que parto para el denominador. Ahora hago la operación y “simplifico” las unidades:

Multiplicando/dividiendo por las potencias de 10 que permitan llegar de la unidad de medida inicial a la final

La escalera es similar, sólo que si se va de un escalón superior a uno inferior, se multiplica por 100 una vez por cada escalón. Si se va de un escalón inferior a uno superior, se divide entre 100 una vez por cada escalón, de esta manera:

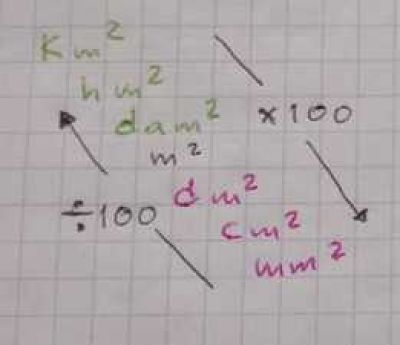
Por lo tanto, para convertir 35 cm² a metros cuadrados se necesita ir del “escalón” cm² al “escalón” m². Son 2 escalones, por lo tanto se divide entre 100 dos veces, que equivale a mover el punto decimal 4 posiciones hacia la izquierda.

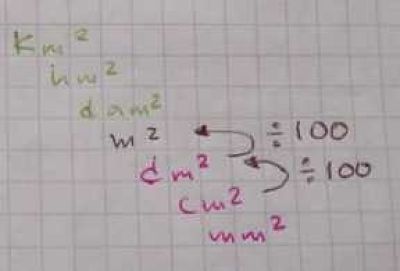
35 cm² = 0.0035 m²

Unidades de volumen en el Sistema Internacional de Unidades:

Las unidades de volumen son los cubos de las unidades de longitud, por lo que las conversiones entre múltiplos y submúltiplos van de 1000 en 1000.

Vean esta comparación de imágenes:

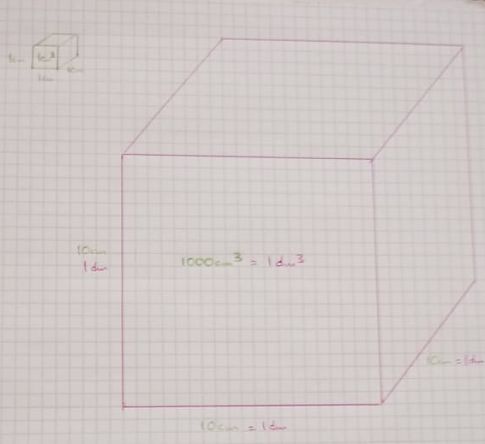
Veamos cómo funcionaría todo lo anterior con medidas de volumen:

1 kilómetro cúbico (km³) = 1 000 000 000 metros cúbicos        1 m³ = 0.000000001 km³
1 hectómetro cúbico (hm³) = 1 000 000 metros cúbicos             1 m³ = 0.000001 hm³
1 decámetro cúbico (dam³) = 1000 metros cúbicos                   1 m³ = 0.001 dam³
1 metro cúbico (m³) = 1 metro cúbico                                            1 m³ = 1 m³
1 decímetro cúbico (dm³) = 0.001 metros cúbicos                      1 m³ = 1 000 dm³
1 centímetro cúbico (cm³) = 0.000001 metros cúbicos              1 m³ = 1 000 000 cm³
1 milímetro cúbico (mm³) = 0.000000001 metros cúbicos        1 m³ = 1 000 000 000 mm³

Conversiones de unidades de volumen en el Sistema Internacional de Unidades:

Como regla de tres directa

Si queremos convertir 35 cm³ a m³

Preparamos las dos columnas y elegimos (si la tenemos) la equivalencia que nos permita multiplicar:

cm³          m³
1               0.000001
35            ?

? = 35 x 0.000001 / 1 = 0.000035 -> 35 cm³ = 0.000035 m³

Pueden ver que si hubieran elegido la otra equivalencia llegan a la misma respuesta:

cm³                m³
1000000         1
35                    ?

? = 35 x 1 / 1000000 = 0.000035 -> 35 cm³ = 0.000035 m³

Multiplicando por la unidad

Convertir 35 cm³ a m³

Escribo los 35 cm³ y luego los multiplico por el 1 formado por la equivalencia de 1 cm³ = 0.000001 m³ . Elijo la unidad a la que quiero llegar para el numerador y la unidad de la que parto para el denominador. Ahora hago la operación y “simplifico” las unidades:

Multiplicando/dividiendo por las potencias de 10 que permitan llegar de la unidad de medida inicial a la final

La escalera es similar, sólo que si se va de un escalón superior a uno inferior, se multiplica por 1000 una vez por cada escalón. Si se va de un escalón inferior a uno superior, se divide entre 1000 una vez por cada escalón, de esta manera:

Por lo tanto, para convertir 35 cm³ a m³ se necesita ir del “escalón” cm³ al “escalón” m³, son 2 escalones, por lo tanto se divide entre 1000 dos veces, que equivale a mover el punto decimal 6 posiciones hacia la izquierda.

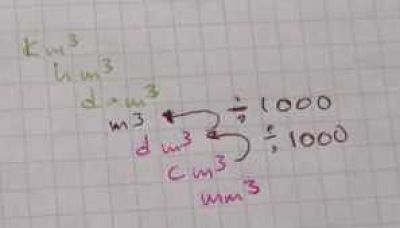
35 cm³ = 0.000035 m³

Unidad de volumen alternativa (capacidad): los litros

Debemos tener cuidado con las conversiones en litros, sobre todo si un problema tiene, por ejemplo, datos en centímetros y piden respuestas en litros, o al revés. Veamos las equivalencias entre los múltiplos y submúltiplos del litro, que son como las del metro:

1 kilolitro (kl) = 1000 litros                         1 l = 0.001 kl
1 hectolitro (hl) = 100 litros                        1 l = 0.01 hl
1 decalitro (dal) = 10 litros                          1 l = 0.1 dal
1 litro (l) = 1 litro                                            1 l = 1 l
1 decilitro (dl) = 0.1 litros                            1 l = 10 dl
1 centilitro (cl) = 0.01 litros                         1 l = 100 cl
1 mililitro (ml) = 0.001 litros                       1 l = 1000 ml

Vean ahora estas equivalencias: la básica es la primera, y de ahí se pueden inferir todas las demás. Escribí un par más para que se vea que no es tan directa la relación.

1 kl = 1 m³ = 1000 dm³= 1000 000 cm³
1 l = 1 dm³ = 0.001 m³ = 1000 cm³
1 cl = 1 cm³ = 0.001 dm³

Para convertir de kilolitro a centilitro se mueve el punto decimal 6 lugares, mientras que de m³ a cm³ podría pensarse que sólo se mueve 2 (m->cm), pero, al multiplicarse por 3 por ser una unidad cúbica, se entiende que son las mismas 6 posiciones.

Unidades de masa dentro del Sistema Internacional de Unidades:

Aquí pasa algo un poco extraño, porque la unidad base para la masa, de la que existe un “patrón” de referencia, es el kilogramo, según vimos al inicio de la entrada. Sin embargo un kilogramo son 1000 gramos y un gramo son 1000 miligramos, por lo que lo lógico sería que la unidad base fuese el gramo. Por convención internacional no es el gramo, sino el kilogramo y todos necesitamos atenernos a las convenciones internacionales para poder entendernos. Pero eso es sólo para el patrón de referencia, no afecta para comprender y realizar las conversiones que veremos aquí.

Otra situación particular es que, como ven, el kilogramo de esta sección es una unidad de masa, no de peso y la mayoría de las veces en la educación primaria se menciona que algo pesa tantos kilogramos o tantos gramos.

Masa y peso son diferentes propiedades físicas. La masa es una medida de la cantidad de materia de un cuerpo. El peso es una medida de la fuerza que es causada sobre el cuerpo por el campo gravitatorio de otro (la Tierra en el caso de los objetos que se mencionan en la primaria).

Se pueden usar indistintamente bajo ciertas circunstancias, en las que se asume que 1 kilogramo de masa pesa 1 kilogramo de peso. Ya en problemas más específicos de física y/o química sí es necesario tener clara la diferencia y tomarla en cuenta.

Esta es la tabla de equivalencias con el gramo como unidad central, con sus múltiplos y submúltiplos:

1 kilgramo (kg) = 1000 gramos                1 g = 0.001 kg
1 hectogramo (hg) = 100 gramos             1 g = 0.01 hg
1 decagramo (dag) = 10 gramos              1 g = 0.1 dag
1 gramo (g) = 1 gramo                                1 g = 1 g
1 decigramo (dg) = 0.1 gramos                1 g = 10 dg
1 centigramo (cg) = 0.01 gramos             1 g = 100 cg
1 milgramo (mg) = 0.001 gramos            1 g = 1000 mg

En este caso todos los procedimientos son prácticamente idénticos a las conversiones con metros.

Como regla de tres directa

Si queremos convertir 35 cg a g

Preparamos las dos columnas y elegimos (si la tenemos) la equivalencia que nos permita multiplicar:

cg     g
1       0.01
35     ?

? = 35 x 0.01 / 1 = 0.35 -> 35 cg = 0.35 g

Como antes, pueden ver que si hubieran elegido la otra equivalencia llegan a la misma respuesta:

cg           g
100         1
35           ?

? = 35 x 1 / 100 = 0. 35 -> 35 cg = 0. 35 g

Multiplicando por la unidad

Convertir 35 cg a g

Escribo los 35 cg y luego los multiplico por el 1 formado por la equivalencia de 1 cg = 0.01 g. Elijo la unidad a la que quiero llegar para el numerador y la unidad de la que parto para el denominador. Ahora hago la operación y “simplifico” las unidades:

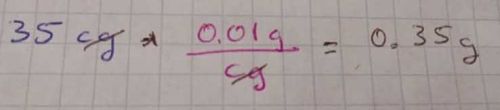
Multiplicando/dividiendo por las potencias de 10 que permitan llegar de la unidad de medida inicial a la final

La escalera es similar, al ir de un escalón superior a uno inferior, se multiplica por 10 una vez por cada escalón. Si se va de un escalón inferior a uno superior, se divide entre 10 una vez por cada escalón, de esta manera:

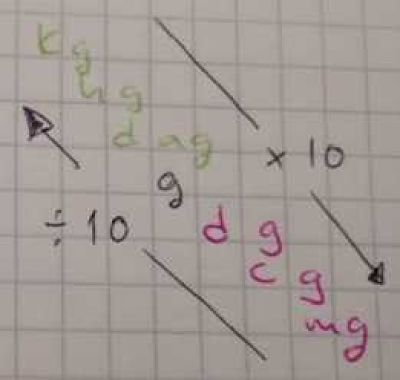
Por lo tanto, para convertir 35 cg a g se necesita ir del “escalón” cg al “escalón” g, son 2 escalones, por lo tanto se divide entre 10 dos veces, que equivale a mover el punto decimal 2 posiciones hacia la izquierda.

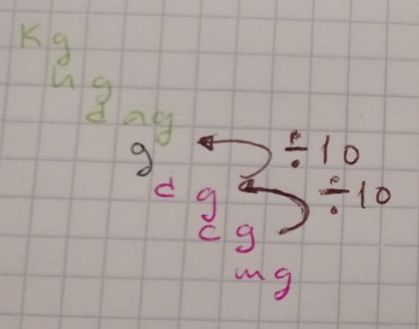
Para cerrar

La siguiente entrada será la 63 y, como es múltiplo de 9 (un número que me encanta por ser muy especial, ver porqué aquí), la dedicaré a un tema especial. En la entrada 64 retomaré las conversiones entre unidades de medida, para complementar ésta, tanto con los procesos para realizar ciertas conversiones menos directas (como la temperatura) como con los cuidados o estrategias que podemos usar al enseñar este tema a nuestros hijos y alumnos.

Antes de irme quiero comentar que usé los mismos números a lo largo de toda la entrada por una estrategia pedagógica que sugiere que se mantenga constante aquello que no es lo que se busca que sea discernido, y se haga variar sólo aquello que se desea que el lector, alumno, hijo, etcétera aprenda. De esa forma se concentra la atención en las variaciones que son trascendentes para distinguir un proceso de otro. La teoría pedagógica que sustenta esta estrategia es la Teoría de la Variación, de Ference Marton.

Como siempre, gracias por leer y compartir.

¡Hasta el siguiente miércoles!

Rebeca

PD1: Aún no he logrado insertar en esta sección un botón que permita seguir el blog… lamento la molestia que implica ir a la página principal para hacerlo.

PD2: Quiero agradecer a estas páginas en las que me apoyo constantemente para redactar el blog: pixabay y webresizer

Anexo para quien tenga curiosidad de conocer cómo se definen las unidades base, según la Conferencia General de Pesas y Medidas:

El metro (m) se define como la longitud de la trayectoria recorrida por la luz en el vacío en un lapso de 1 / 299 792 458 de segundo (17ª Conferencia General de Pesas y Medidas de 1983).

El kilogramo (kg) se define como la masa igual a la del prototipo internacional del kilogramo (1ª y 3ª Conferencia General de Pesas y Medidas, 1889 y 1901).

El segundo (s) se define como la duración de 9 192 631 770 períodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado base del átomo de cesio 133 (13ª Conferencia General de Pesas y Medidas, 1967).

El ampere (A) se define como la intensidad de una corriente constante, que mantenida en dos conductores paralelos, rectilíneos, de longitud infinita, de sección circular despreciable, colocados a un metro de distancia entre sí en el vacío, produciría entre estos conductores una fuerza igual a 2 X 10-7 newton por metro de longitud (9ª Conferencia General de Pesas y Medidas, 1948).

El kelvin (K) se define como la fracción 1/273,16 de la temperatura termodinámica del punto triple del agua (13ª Conferencia General de Pesas y Medidas, 1967).

El mol (mol) se define como la cantidad de materia que contiene tantas unidades elementales como átomos existen en 0,012 kilogramos de carbono 12 (12C) (14ª Conferencia General de Pesas y Medidas, 1971).

La candela (cd) se define como la intensidad luminosa, en una dirección dada de una fuente que emite una radiación monocromática de frecuencia 540 x 1012 Hz y cuya intensidad energética en esa dirección es de 1/683 wat por esterradián (16ª Conferencia General de Pesas y Medidas, 1979).

Tomado de: http://www.cenam.mx/siu.aspx